
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】百子回归图是由1,2,3,100无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四位“19991220”表示澳门回归祖国日期,最后一行中间两位“2350”表示澳门面积,…,同时它也是十阶幻方,其每行10个数之和,每列10个数之和,以及两条对角线上10个数之和均为有理数n,则4n﹣1的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
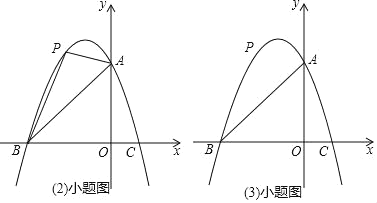
【题目】已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉﹣﹣明白玉幻方.其背面有方框四行十六格,为四阶幻方(从1到16,一共十六个数目,它们的纵列、横行与两条对角线上4个数相加之和均为34).小明探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数a,b,c,d有如图1的位置关系时,均有a+b=c+d=17.如图2,已知此幻方中的一些数,则x的值为__.
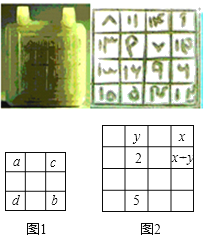
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() r,则称点P为⊙O的“随心点”.
r,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(4,0),B(0,3),C(![]() ,﹣
,﹣![]() ),D(﹣
),D(﹣![]() ,﹣2)中,⊙O的“随心点”是 ;
,﹣2)中,⊙O的“随心点”是 ;
(2)若点E(6,8)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=4时,直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三点,其中t>0,函数![]() 的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.
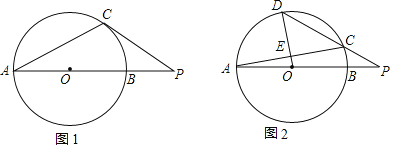
(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,甲、乙两人分别从![]() 两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在
两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在![]() 之间的
之间的![]() 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回![]() 地,乙继续向
地,乙继续向![]() 地前行.甲到达
地前行.甲到达![]() 地时停止行走,乙到达
地时停止行走,乙到达![]() 地是也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
地是也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的关系如图所示,则下列结论错误的是( )
(分钟)之间的关系如图所示,则下列结论错误的是( )
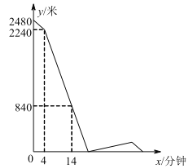
A.![]() 两地相距2480米B.甲的速度是60米/分钟,乙的速度是80米/分钟
两地相距2480米B.甲的速度是60米/分钟,乙的速度是80米/分钟
C.乙出发17分钟后,两人在![]() 地相遇D.乙到达
地相遇D.乙到达![]() 地时,甲与
地时,甲与![]() 地相距的路程是300米.
地相距的路程是300米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com