
【题目】如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.
(1)若∠G=48°,求∠ACB的度数;
(2)若AB=AE,求证:∠BAD=∠COF;
(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=![]() ,求
,求![]() 的值.
的值.

【答案】(1)48°(2)证明见解析(3)![]()
【解析】
(1)连接CD,根据圆周角定理和垂直的定义可得结论;
(2)先根据等腰三角形的性质得:∠ABE=∠AEB,再证明∠BCG=∠DAC,可得 ![]() ,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;
,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;
(3)过O作OG⊥AB于G,证明△COF≌△OAG,则OG=CF=x,AG=OF,设OF=a,则OA=OC=2x-a,根据勾股定理列方程得:(2x-a)2=x2+a2,则a=![]() x,代入面积公式可得结论.
x,代入面积公式可得结论.
(1)连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠ACB+∠BCD=90°,
∵AD⊥CG,
∴∠AFG=∠G+∠BAD=90°,
∵∠BAD=∠BCD,
∴∠ACB=∠G=48°;
(2)∵AB=AE,
∴∠ABE=∠AEB,
∵∠ABC=∠G+∠BCG,∠AEB=∠ACB+∠DAC,
由(1)得:∠G=∠ACB,
∴∠BCG=∠DAC,
∴![]() ,
,
∵AD是⊙O的直径,AD⊥PC,
∴![]() ,
,
∴![]() ,
,
∴∠BAD=2∠DAC,
∵∠COF=2∠DAC,
∴∠BAD=∠COF;
(3)过O作OG⊥AB于G,设CF=x,
∵tan∠CAF=![]() =
=![]() ,
,
∴AF=2x,
∵OC=OA,由(2)得:∠COF=∠OAG,
∵∠OFC=∠AGO=90°,
∴△COF≌△OAG,
∴OG=CF=x,AG=OF,
设OF=a,则OA=OC=2x﹣a,
Rt△COF中,CO2=CF2+OF2,
∴(2x﹣a)2=x2+a2,
a=![]() x,
x,
∴OF=AG=![]() x,
x,
∵OA=OB,OG⊥AB,
∴AB=2AG=![]() x,
x,
∴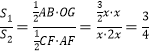 .
.


科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①两边及其中一边上的中线对应相等的两个三角形全等;②两边及其中一边上的高对应相等的两个三角形全等;③两边及一角对应相等的两个三角形全等;④有两角及其中一角的角平分线对应相等的两个三角形全等.其中正确的的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),有A、B、C三种不同型号的卡片若干张,其中A型是边长为a(a>b)的正方形,B型是长为a、宽为b的长方形,C型是边长为b的正方形.

(1)若用A型卡片1张,B型卡片2张,C型卡片1张拼成了一个正方形(如图(2)),此正方形的边长为 ,根据该图形请写出一条属于因式分解的等式: .
(2)若要拼一个长为2a+b,宽为a+2b的长方形,设需要A类卡片x张,B类卡片y张,C类卡片z张,则x+y+z= .
(3)现有A型卡片1张,B型卡片6张,C型卡片11张,从这18张卡片中拿掉两张卡片,余下的卡片全用上,你能拼出一个长方形或正方形吗?有几种拼法?请你通过运算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间 x(单位:h)变化的图象如图所示,

根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“国家卫生城市”复检,某市环卫局准备购买![]() 、
、![]() 两种型号的垃圾箱,通过市场调研得知:购买3个
两种型号的垃圾箱,通过市场调研得知:购买3个![]() 型垃圾箱和2个
型垃圾箱和2个![]() 型垃圾箱共需540元;购买2个
型垃圾箱共需540元;购买2个![]() 型垃圾箱比购买3个
型垃圾箱比购买3个![]() 型垃圾箱少用160元.
型垃圾箱少用160元.
(1)每个![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱各多少元?
型垃圾箱各多少元?
(2)现需要购买![]() ,
,![]() 两种型号的垃圾箱共300个,设购买
两种型号的垃圾箱共300个,设购买![]() 型垃圾箱
型垃圾箱![]() 个,购买
个,购买![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱的总费用为
型垃圾箱的总费用为![]() 元,求
元,求![]() 与
与![]() 的函数表达式.如果购买
的函数表达式.如果购买![]() 型垃圾箱是
型垃圾箱是![]() 型垃圾箱的2倍,求购买
型垃圾箱的2倍,求购买![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱的总费用.
型垃圾箱的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
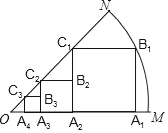
【题目】如图所示,扇形OMN的圆心角为45°,正方形A1B1C1A2的边长为2,顶点A1,A2在线段OM上,顶点B1在弧MN上,顶点C1在线段ON上,在边A2C1上取点B2,以A2B2为边长继续作正方形A2B2C2A3,使得点C2在线段ON上,点A3在线段OM上,……,依次规律,继续作正方形,则A2018M=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com