
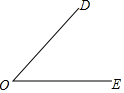
 如图,∠DOE=48°,OD平分∠AOC,∠AOC=60°,OE平分∠BOC,请你用直尺,量角器补全图形并求∠BOC的度数.
如图,∠DOE=48°,OD平分∠AOC,∠AOC=60°,OE平分∠BOC,请你用直尺,量角器补全图形并求∠BOC的度数. 分析 要分两种情况讨论:当射线OC在∠DOE内部时,当射线OC在∠DOE外部时,分别画出图形,再根据角平分线定义、角的和差关系计算即可.
解答 解:①当射线OC在∠DOE内部时,射线OA,OB,OC的位置如图1所示,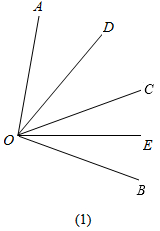
∵OD平分∠AOC,∠AOC=60°,
∴∠AOD=∠DOC=30°,
∵∠DOE=48°,
∴∠EOC=∠DOE-∠DOC=18°,
∵OE平分∠BOC,
∴∠BOE=∠EOC=18°,
∴∠BOC=∠EOC+∠BOE=36°;
②当射线OC在∠DOE外部时,射线OA,OB,OC的位置如图2所示,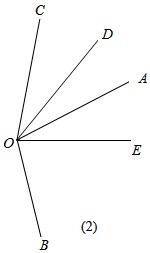
∵OD平分∠AOC,∠AOC=60°,
∴∠AOD=∠DOC=30°,
∵∠DOE=48°,
∴∠EOC=∠DOE+∠DOC=78°,
∵OE平分∠BOC,
∴∠BOE=∠EOC=78°,
∴∠BOC=∠EOC+∠BOE=156°.
点评 本题注意考查了基本作图和复杂作图,以及角度的计算,主要利用了角平分线的定义进行计算,先确定出∠COD的度数是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
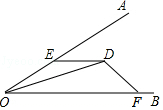 如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,
如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
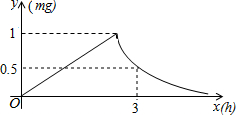 为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.
为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com