
【题目】如图,直线y=k1x+b(k1≠0)与双曲线y= ![]() (k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点. 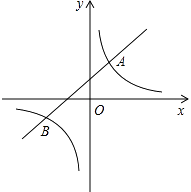
(1)求直线和双曲线的解析式.
(2)若A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三点,且x1<x2<0<x3 , 请直接写出y1 , y2 , y3的大小关系式.
【答案】
(1)解:∵双曲线y= ![]() 经过点B(﹣2,﹣1),
经过点B(﹣2,﹣1),
∴k2=2,
∴双曲线的解析式为:y= ![]() ,
,
∵点A(1,m)在双曲线y= ![]() 上,
上,
∴m=2,即A(1,2),
由点A(1,2),B(﹣2,﹣1)在直线y=k1x+b上,得 ![]() ,
,
解得: ![]() ,
,
∴直线的解析式为:y=x+1
(2)解:∵A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,
∴A1与A2在第三象限,A3在第一象限,即y1<0,y2<0,y3>0,
则y2<y1<y3
【解析】(1)将B坐标代入双曲线解析式求出k2的值,确定出反比例解析式,将A坐标代入反比例解析式求出m的值,确定出A的坐标,将A与B坐标代入直线解析式求出k1与b的值,即可确定出直线解析式;(2)先根据横坐标的正负分象限,再根据反比例函数的增减性判断即可.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,O为原点,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0.
![]()
(1)a=________,b=_________;
(2)若点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(秒).
①当点P运动到线段OB上,且PO=2PB时,求t的值;
②先取OB的中点E,当点P在线段OE上时,再取AP的中点F,试探究![]() 的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
③若点P从点A出发,同时,另一动点Q从点B出发,以每秒2个单位长度的速度向左匀速运动,到达点O后立即原速返回向右匀速运动,当PQ=1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道(通道面积不超过总面积的![]() ),其余部分铺上草皮.
),其余部分铺上草皮.
(1)如图1,若设计两条通道,一条横向,一条纵向,4块草坪为全等的长方形,每块草坪的两边之比为3:4,并且纵向通道的宽度是横向通道宽度的2倍,问横向通道的宽是多少?
(2)如图2,为设计得更美观,其中草坪①②③④为全等的正方形,草坪⑤⑥为全等的长方形(两边长BN:BM=2:3),通道宽度都相等,问:此时通道的宽度又是多少呢?
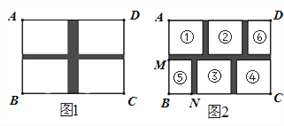
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,直角边AB=6,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
(x>0)的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 . 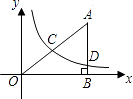
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价60元,厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款.
现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若按方案①购买夹克和T恤共需 元(用含x的式子表示),若按方案②购买夹克和T恤共需 元(用含x的式子表示)
(2)若x=40,通过计算说明按方案①,②,哪种方案购买较为合算?
(3)当购买多少件T恤时,按以上两种方案购买所付价钱一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
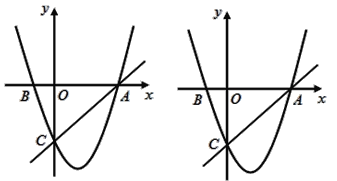
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com