
”¾ĢāÄæ”æČēĶ¼ŹĒÅ×ĪļĻßy1=ax2+bx+c£Øa”Ł0£©Ķ¼ĻóµÄŅ»²æ·Ö£¬Å×ĪļĻߵĶ„µć×ų±źA£Ø1£¬3£©£¬ÓėxÖįµÄŅ»øö½»µćB£Ø4£¬0£©£¬Ö±Ļßy2=mx+n£Øm”Ł0£©ÓėÅ×ĪļĻß½»ÓŚA£¬BĮ½µć£¬ĻĀĮŠ½įĀŪ£ŗ ¢Ł2a+b=0£»
¢Śabc£¾0£»
¢Ū·½³Ģax2+bx+c=3ÓŠĮ½øöĻąµČµÄŹµŹżøł£»
¢ÜÅ×ĪļĻßÓėxÖįµÄĮķŅ»øö½»µćŹĒ£Ø©1£¬0£©£»
¢Żµ±1£¼x£¼4Ź±£¬ÓŠy2£¼y1 £¬
ĘäÖŠÕżČ·µÄŹĒ£Ø £©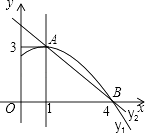
A.¢Ł¢Ś¢Ū
B.¢Ł¢Ū¢Ü
C.¢Ł¢Ū¢Ż
D.¢Ś¢Ü¢Ż
”¾“š°ø”æC
”¾½āĪö”æ½ā£ŗ”ßÅ×ĪļĻߵĶ„µć×ų±źA£Ø1£¬3£©£¬ ”ąÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=© ![]() =1£¬
=1£¬
”ą2a+b=0£¬ĖłŅŌ¢ŁÕżČ·£»
”ßÅ×ĪļĻßæŖæŚĻņĻĀ£¬
”ąa£¼0£¬
”ąb=©2a£¾0£¬
”ßÅ×ĪļĻßÓėyÖįµÄ½»µćŌŚxÖįÉĻ·½£¬
”ąc£¾0£¬
”ąabc£¼0£¬ĖłŅŌ¢Ś“ķĪó£»
”ßÅ×ĪļĻߵĶ„µć×ų±źA£Ø1£¬3£©£¬
”ąx=1Ź±£¬¶ž“ĪŗÆŹżÓŠ×ī“óÖµ£¬
”ą·½³Ģax2+bx+c=3ÓŠĮ½øöĻąµČµÄŹµŹżøł£¬ĖłŅŌ¢ŪÕżČ·£»
”ßÅ×ĪļĻßÓėxÖįµÄŅ»øö½»µćĪŖ£Ø4£¬0£©
¶ųÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=1£¬
”ąÅ×ĪļĻßÓėxÖįµÄĮķŅ»øö½»µćĪŖ£Ø©2£¬0£©£¬ĖłŅŌ¢Ü“ķĪó£»
”ßÅ×ĪļĻßy1=ax2+bx+cÓėÖ±Ļßy2=mx+n£Øm”Ł0£©½»ÓŚA£Ø1£¬3£©£¬Bµć£Ø4£¬0£©
”ąµ±1£¼x£¼4Ź±£¬y2£¼y1 £¬ ĖłŅŌ¢ŻÕżČ·£®
¹ŹŃ”£ŗC£®
”¾æ¼µć¾«Īö”æ½ā“š“ĖĢāµÄ¹Ų¼üŌŚÓŚĄķ½ā¶ž“ĪŗÆŹżĶ¼ĻóŅŌ¼°ĻµŹża”¢b”¢cµÄ¹ŲĻµµÄĻą¹ŲÖŖŹ¶£¬ÕĘĪÕ¶ž“ĪŗÆŹży=ax2+bx+cÖŠ£¬a”¢b”¢cµÄŗ¬Ņå£ŗa±ķŹ¾æŖæŚ·½Ļņ£ŗa>0Ź±£¬Å×ĪļĻßæŖæŚĻņÉĻ; a<0Ź±£¬Å×ĪļĻßæŖæŚĻņĻĀbÓė¶Ō³ĘÖįÓŠ¹Ų£ŗ¶Ō³ĘÖįĪŖx=-b/2a;c±ķŹ¾Å×ĪļĻßÓėyÖįµÄ½»µć×ų±ź£ŗ£Ø0£¬c£©£¬ŅŌ¼°¶ŌÅ×ĪļĻßÓė×ų±źÖįµÄ½»µćµÄĄķ½ā£¬ĮĖ½āŅ»ŌŖ¶ž“Ī·½³ĢµÄ½āŹĒĘä¶ŌÓ¦µÄ¶ž“ĪŗÆŹżµÄĶ¼ĻńÓėxÖįµÄ½»µć×ų±ź£®Ņņ“ĖŅ»ŌŖ¶ž“Ī·½³ĢÖŠµÄb2-4ac£¬ŌŚ¶ž“ĪŗÆŹżÖŠ±ķŹ¾Ķ¼ĻńÓėxÖįŹĒ·ńÓŠ½»µć£®µ±b2-4ac>0Ź±£¬Ķ¼ĻńÓėxÖįÓŠĮ½øö½»µć£»µ±b2-4ac=0Ź±£¬Ķ¼ĻńÓėxÖįÓŠŅ»øö½»µć£»µ±b2-4ac<0Ź±£¬Ķ¼ĻńÓėxÖįƻӊ½»µć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży£½kx£«b(k”Ł0)µÄĶ¼ĻóÓėxÖįµÄ½»µć×ų±źĪŖ(£2£¬0)£¬ŌņĻĀĮŠĖµ·Ø£ŗ¢ŁyĖęxµÄŌö“ó¶ų¼õŠ”£»¢Ś¹ŲÓŚxµÄ·½³Ģkx£«b£½0µÄ½āĪŖx£½£2£»¢Ūkx£«b£¾0µÄ½ā¼ÆŹĒx£¾£2£»¢Üb£¼0.ĘäÖŠÕżČ·µÄÓŠ__________£®(ĢīŠņŗÅ)

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c£¬OA=OC£¬ĻĀĮŠ¹ŲĻµÖŠÕżČ·µÄŹĒ£Ø £©
A.ac+1=b
B.ab+1=c
C.bc+1=a
D.![]()
+1=c
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¼1ŹĒ±ß³¤·Ö±šĪŖ4 ![]() ŗĶ2µÄĮ½øöµČ±ßČż½ĒŠĪÖ½Ę¬ABCŗĶOD”äE”䵞·ÅŌŚŅ»Ęš£ØCÓėOÖŲŗĻ£©£®
ŗĶ2µÄĮ½øöµČ±ßČż½ĒŠĪÖ½Ę¬ABCŗĶOD”äE”䵞·ÅŌŚŅ»Ęš£ØCÓėOÖŲŗĻ£©£® 
£Ø1£©²Ł×÷£ŗ¹Ģ¶Ø”÷ABC£¬½«”÷ODEČʵćCĖ³Ź±ÕėŠż×Ŗ30”ć£¬ŗóµĆµ½”÷ODE£¬Į¬½ÓAD”¢BE”¢CEµÄŃÓ³¤Ļß½»ABÓŚF£ØĶ¼2£©£ŗ Ģ½¾æ£ŗŌŚĶ¼2ÖŠ£¬Ļ߶ĪBEÓėADÖ®¼äÓŠŌõŃłµÄ“󊔹ŲĻµ£æŹŌÖ¤Ć÷ÄćµÄ½įĀŪ£®
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ½«”÷ODE£¬ŌŚĻ߶ĪCFÉĻŃŲ×ÅCF·½ĻņŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĘ½ŅĘ£¬Ę½ŅĘŗóµÄ”÷CDEÉčĪŖ”÷PQR£¬µ±µćPÓėµćFÖŲŗĻŹ±Ķ£Ö¹ŌĖ¶Æ£ØĶ¼3£©£® Ģ½¾æ£ŗÉč”÷PQRŅĘ¶ÆµÄŹ±¼äĪŖxĆė£¬”÷PQRÓė”÷ABCÖŲµž²æ·ÖµÄĆ껿ĪŖy£¬ĒóyÓėxÖ®¼äµÄŗÆŹż½āĪöŹ½£¬²¢Š“³öŗÆŹż×Ō±äĮæxµÄȔֵ·¶Ī§£®
£Ø3£©½«Ķ¼1ÖŠ”÷ODE¹Ģ¶Ø£¬°Ń”÷ABCŃŲ×ÅOE·½ĻņĘ½ŅĘ£¬Ź¹¶„µćCĀäŌŚOEµÄÖŠµćG“¦£¬ÉčĪŖ”÷ABG£¬Č»ŗó½±”÷ABGČʵćGĖ³Ź±ÕėŠż×Ŗ£¬±ßBG½»±ßDEÓŚµćM£¬±ßAG½»±ßDOÓŚµćN£¬Éč”ĻBGE=¦Į£Ø30”ć£¼¦Į£¼90”ć£©£ØĶ¼4£©£® Ģ½¾æ£ŗŌŚĶ¼4ÖŠ£¬Ļ߶ĪONEMµÄÖµŹĒ·ńĖę¦ĮµÄ±ä»Æ¶ų±ä»Æ£æČē¹ūƻӊ±ä»Æ£¬ĒėÄćĒó³öONEMµÄÖµ£¬Čē¹ūÓŠ±ä»Æ£¬ĒėÄćĖµĆ÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹżÓė·“±ČĄżŗÆŹżµÄĶ¼ĻóĻą½»ÓŚA”¢BĮ½µć£¬ŌņĶ¼ÖŠŹ¹·“±ČĄżŗÆŹżµÄÖµŠ”ÓŚŅ»“ĪŗÆŹżµÄÖµµÄxµÄȔֵ·¶Ī§ŹĒ£Ø £© 
A.x£¼©1
B.x£¾2
C.©1£¼x£¼0£¬»ņx£¾2
D.x£¼©1£¬»ņ0£¼x£¼2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪOABCµÄ¶„µćA”¢CµÄ×ų±ź·Ö±šŹĒ£Ø4£¬0£©ŗĶ£Ø0£¬2£©£¬·“±ČĄżŗÆŹży= ![]() £Øx£¾0£©µÄĶ¼Ļó¹ż¶Ō½ĒĻߵĽ»µćP²¢ĒŅÓėAB£¬BC·Ö±š½»ÓŚD£¬EĮ½µć£¬Į¬½ÓOD£¬OE£¬DE£¬Ōņ”÷ODEµÄĆ껿ĪŖ £®
£Øx£¾0£©µÄĶ¼Ļó¹ż¶Ō½ĒĻߵĽ»µćP²¢ĒŅÓėAB£¬BC·Ö±š½»ÓŚD£¬EĮ½µć£¬Į¬½ÓOD£¬OE£¬DE£¬Ōņ”÷ODEµÄĆ껿ĪŖ £® 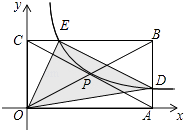
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
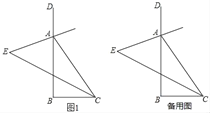
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼£Ø1£©£¬ŅŃÖŖ£ŗŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬AB=AC£¬Ö±Ļßm¾¹żµćA£¬BD”ĶÖ±Ļßm, CE”ĶÖ±Ļßm,“¹×ć·Ö±šĪŖµćD”¢E.Ö¤Ć÷:DE=BD+CE.
£Ø2£© ČēĶ¼£Ø2£©£¬½«£Ø1£©ÖŠµÄĢõ¼žøÄĪŖ£ŗŌŚ”÷ABCÖŠ£¬AB=AC£¬D”¢A”¢EČżµć¶¼ŌŚÖ±ĻßmÉĻ,²¢ĒŅÓŠ”ĻBDA=”ĻAEC=”ĻBAC=![]() ,ĘäÖŠ
,ĘäÖŠ![]() ĪŖČĪŅāČń½Ē»ņ¶Ū½Ē.ĒėĪŹ½įĀŪDE=BD+CEŹĒ·ń³ÉĮ¢?Čē³ÉĮ¢,ĒėÄćøų³öÖ¤Ć÷;Čō²»³ÉĮ¢,ĒėĖµĆ÷ĄķÓÉ.
ĪŖČĪŅāČń½Ē»ņ¶Ū½Ē.ĒėĪŹ½įĀŪDE=BD+CEŹĒ·ń³ÉĮ¢?Čē³ÉĮ¢,ĒėÄćøų³öÖ¤Ć÷;Čō²»³ÉĮ¢,ĒėĖµĆ÷ĄķÓÉ.
£Ø3£©ĶŲÕ¹ÓėÓ¦ÓĆ£ŗČēĶ¼£Ø3£©£¬D”¢EŹĒD”¢A”¢EČżµćĖłŌŚÖ±ĻßmÉĻµÄĮ½¶Æµć£ØD”¢A”¢EČżµć»„²»ÖŲŗĻ£©,µćFĪŖ”ĻBACĘ½·ÖĻßÉĻµÄŅ»µć,ĒŅ”÷ABFŗĶ”÷ACF¾łĪŖµČ±ßČż½ĒŠĪ£¬Į¬½ÓBD”¢CE,Čō”ĻBDA=”ĻAEC=”ĻBAC£¬ŹŌÅŠ¶Ļ”÷DEFµÄŠĪד.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ”÷ABCµÄČżøö¶„µćµÄ×ų±ź·Ö±šĪŖA£Ø©3£¬5£©£¬B£Ø©2£¬1£©£¬C£Ø©1£¬3£©£®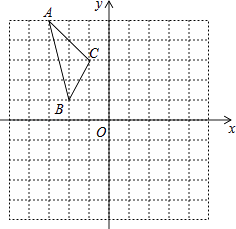
£Ø1£©Čō”÷ABC¾¹żĘ½ŅĘŗóµĆµ½”÷A1B1C1 £¬ ŅŃÖŖµćC1µÄ×ų±źĪŖ£Ø4£¬0£©£¬Š“³ö¶„µćA1 £¬ B1µÄ×ų±ź£»
£Ø2£©Čō”÷ABCŗĶ”÷A2B2C2¹ŲÓŚŌµćO³ÉÖŠŠÄ¶Ō³ĘĶ¼ŠĪ£¬Š“³ö”÷A2B2C2µÄø÷¶„µćµÄ×ų±ź£»
£Ø3£©½«”÷ABCČĘ×ŵćO°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćµĆµ½”÷A3B3C3 £¬ Š“³ö”÷A3B3C3µÄø÷¶„µćµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻB=90”ć£¬·Ö±š×÷ĘäÄŚ½Ē”ĻACBÓėĶā½Ē”ĻDACµÄĘ½·ÖĻߣ¬ĒŅĮ½Ģõ½ĒĘ½·ÖĻßĖłŌŚµÄÖ±Ļß½»ÓŚµćE£®
£Ø1£©”ĻE=”” ”””ć£»
£Ø2£©·Ö±š×÷”ĻEABÓė”ĻECBµÄĘ½·ÖĻߣ¬ĒŅĮ½Ģõ½ĒĘ½·ÖĻß½»ÓŚµćF£®
¢ŁŅĄĢāŅāŌŚĶ¼1ÖŠ²¹Č«Ķ¼ŠĪ£»
¢ŚĒó”ĻAFCµÄ¶ČŹż£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ÉäĻßFMŌŚ”ĻAFCµÄÄŚ²æĒŅ”ĻAFM=![]() ”ĻAFC£¬ÉčECÓėABµÄ½»µćĪŖH£¬ÉäĻßHNŌŚ”ĻAHCµÄÄŚ²æĒŅ”ĻAHN=
”ĻAFC£¬ÉčECÓėABµÄ½»µćĪŖH£¬ÉäĻßHNŌŚ”ĻAHCµÄÄŚ²æĒŅ”ĻAHN=![]() ”ĻAHC£¬ÉäĻßHNÓėFM½»ÓŚµćP£¬Čō”ĻFAH£¬”ĻFPHŗĶ”ĻFCHĀś×ćµÄŹżĮæ¹ŲĻµĪŖ”ĻFCH=m”ĻFAH+n”ĻFPH£¬ĒėÖ±½ÓŠ“³öm£¬nµÄÖµ£®
”ĻAHC£¬ÉäĻßHNÓėFM½»ÓŚµćP£¬Čō”ĻFAH£¬”ĻFPHŗĶ”ĻFCHĀś×ćµÄŹżĮæ¹ŲĻµĪŖ”ĻFCH=m”ĻFAH+n”ĻFPH£¬ĒėÖ±½ÓŠ“³öm£¬nµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com