
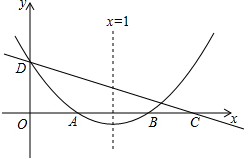
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据抛物线的性质逐项判断即可.由抛物线的开口判断a的符号;由对称轴判断b及b与2a的关系;还可由图象上点的坐标判断.
解答 解:∵抛物线开口向上,
∴a>0.
∵抛物线对称轴是x=1,
∴b<0且b=-2a.
∵抛物线与y轴交于正半轴,
∴c>0.
∴①abc>0错误;
②3a+b>0正确;
∵直线y=kx+c经过一、二、四象限,
∴k<0.
∵OA=OD,
∴点A的坐标为(c,0).
直线y=kx+c当x=c时,y>0,
∴kc+c>0可得k>-1.
∴③-1<k<0正确;
∵直线y=kx+c与抛物线y=ax2+bx+c的图象有两个交点
∴ax2+bx+c=kx+c,
得x1=0,${x}_{2}=\frac{k-b}{a}$,
由图象知x2>1,
∴$\frac{k-b}{a}>1$,
∴k>a+b
∴④k>a+b正确;
∵$\left\{\begin{array}{l}{2a+b=0}\\{c(ac+b+1)=0}\end{array}\right.$,
∴2a-ac=1.
∴ac=2a-1,
∵-1<k<0,
∴⑤令ax2+bx+c=kx+c,
∴ax+b=k,
∵b=-2a,
∴x=$\frac{k+2a}{a}$,
∵交点在B(2-c,0)右边,
∴$\frac{k-2a}{a}$>2-c,
∴k+2a>2a-ac,
∴ac+k>0,故正确.
故选D.
点评 本题主要考查了抛物线的性质,解决本题的关键是利用图象判断系数的符号以及一次函数的性质.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
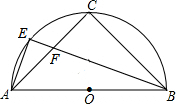 如图,AB是半⊙O的直径,点C是弧AB的中点,点E是弧AC的中点,连结EB、CA交于点F,则$\frac{EF}{BF}$=$\frac{\sqrt{2}-1}{2}$.
如图,AB是半⊙O的直径,点C是弧AB的中点,点E是弧AC的中点,连结EB、CA交于点F,则$\frac{EF}{BF}$=$\frac{\sqrt{2}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
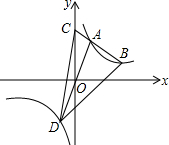 如图,已知直线y=-x+5交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交y轴于C点,AO的延长线交双曲线y=$\frac{k}{x}$(x<0)于D点,且S△BCD=15,则k=6.
如图,已知直线y=-x+5交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交y轴于C点,AO的延长线交双曲线y=$\frac{k}{x}$(x<0)于D点,且S△BCD=15,则k=6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com