



 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
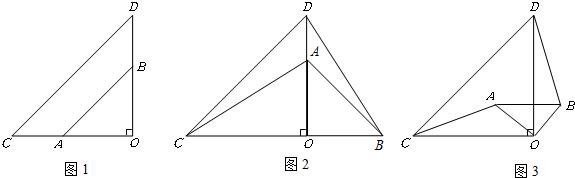
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届江苏省初三第一学期期中考试数学试卷 题型:解答题
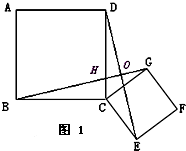
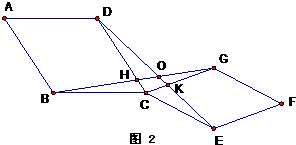
如图甲,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
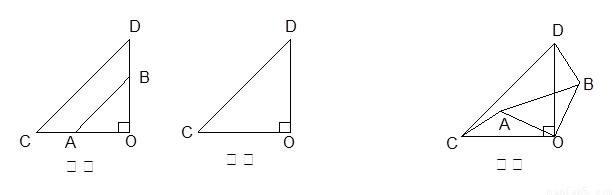
1.在图甲中,你发现线段AC、BD的数量关系是_______,直线AC、BD相交成____度角
2.将图甲中的 绕点O顺时针旋转
绕点O顺时针旋转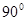 ,在图乙中作出旋转后的
,在图乙中作出旋转后的 ;
;
3.将图甲中的 绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若
绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若 绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com