
【题目】已知∠AOB=108°,∠BOC=22°,射线OD、OE分别是∠AOB和∠BOC的平分线,求∠DOE的度数.
【答案】∠DOE的度数为43°或65°.
【解析】
分两种情况讨论:(1)当OC在∠AOB的内部时;(2)当OC在∠AOB的外部时,分别作出图形,利用角平分线的定义进行角度计算.
(1)当OC在∠AOB的内部时,如图1所示:
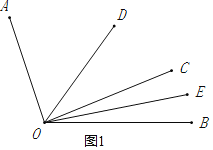
∵OE是∠BOC的平分线,
∴∠BOE=∠COE=![]() ∠BOC,
∠BOC,
又∵∠BOC=22°,
∴∠COE=11°,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD=![]() ∠AOB,
∠AOB,
又∵∠AOB=108°,
∴∠BOD=54°,
又∵∠BOC+∠COD=∠BOD,
∵∠COD=54°﹣22°=32°,
又∵∠DOE=∠DOC+COE,
∴∠DOE=32°+11°=43°;
(2)当OC在∠AOB的外部时,如图2所示:
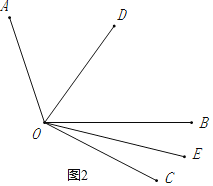
∵OE是∠BOC的平分线,
∴∠BOE=∠COE=![]() ∠BOC,
∠BOC,
又∵∠BOC=22°,
∴∠BOE=11°,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD=![]() ∠AOB,
∠AOB,
又∵∠AOB=108°,
∴∠BOD=54°,
又∵∠DOE=∠BOD+∠BOE,
∴∠DOE=54°+11°=65°;
综合所述,∠DOE的度数为43°或65°.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】武汉二中广雅中学为了了解全校学生的课外阅读的情况,随机抽取了部分学生进行阅读时间调查,现将学生每学期的阅读时间m分成A、B、C、D四个等级(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
(1)C组的人数是 人,并补全条形统计图.
(2)本次调查的众数是 等,中位数落在 等.
(3)国家规定:“中小学每学期的课外阅读时间不低于60小时”,如果该校今年有3500名学生,达到国家规定的阅读时间的人数约有 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着2018年两会的隆重召开,中学校园掀起了关注时事政治的热潮我区及时开展“做一个关心国家大事的中学生”主题活动。为了了解我区中学生获取时事新闻的主要途径,分别从电脑上网、手机上网、听广播、看电视、看报纸五个方面,在全区范围内随机抽取了若干名中学生进行问卷调查(每名中学生只选一种主要途径),根据调查结果绘制了如图所示的不完整的统计图请根据统计图的信息回答下列问题:

(1)本次调查共抽取了中学生多少人?
(2)求本次调查中,以听广播获取时事新闻为主要途径的人数并补全条形统计图;
(3)若本区共有中学生7000人,请你估计我区以看电视以看电视获取时事新闻为主要途径的中学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示数![]() ,点B表示数
,点B表示数![]() ,AB表示点A和点B之间的距离.
,AB表示点A和点B之间的距离.![]() ,
,![]() 满足
满足![]() .
.
(1)在原点O处放了一挡板,若一小球P从点A处以3个单位/秒的速度向左运动,同时另一个小球Q从点B处以4个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反方向运动,设运动时间t(秒),问t为何值时,P、Q两球到原点的距离相等?
(2)若小球P从点A以每秒4个单位的速度向右运动,小球Q同时从点B以每秒3个单位得速度向左运动,则是否存在时间t,使得AP+BQ=2PQ?若存在,请求出时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,O,B是数轴上从左至右的三个点,其中O与原点重合,点A表示的数为﹣4,且AO+AB=11.
![]()
(1)求出点B所表示的数,并在数轴上把点B表示出来.
(2)点C是数轴上的一个点,且CA:CB=1:2,求点C表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E. F.

(1)求证:△OEF是等腰直角三角形。
(2)若AE=4,CF=3,求EF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班全体学生进行了第一次体育中考模拟测试,成绩统计如下表:
成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数(人) | 6 | 5 | 5 | 8 | 7 | 7 | 4 |
根据上表中的信息判断,下列结论中错误的是( )
A. 该班一共有42名同学
B. 该班学生这次考试成绩的众数是8
C. 该班学生这次考试成绩的平均数是27
D. 该班学生这次考试成绩的中位数是27分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)36+(-25)+12+(-15);
(2) 9+(-2.5)+(+6)+(-3.5);
(3)3.7+(-9.1)+6.3+(-0.9) ;
(4)10-(-5)-(-6)-(+18)
(5)(-12)-6-(-8)-(-12);
(6)5-(-5)+(-10)+0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com