
【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

【答案】(1)证明见解析(2)成立
【解析】试题分析:(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DEG,从而得出GE=GF;
(2)结论仍然成立,同理可以证明得到.
试题解析:(1)证明:∵DE⊥AC,BF⊥AC,
∴∠DEF=∠BFE=90°.
∵AE=CF,AE+EF=CF+EF.即AF=CE.
在Rt△ABF和Rt△CDE中, ![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中, 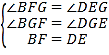 ,
,
∴△BFG≌△DGE(AAS),
∴GE=GF;
(2)结论依然成立.
理由:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°
∵AE=CF
∴AE﹣EF=CF﹣EF,即AF=CE,
在Rt△ABF和Rt△CDE中, ![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF
在△BFG和△DEG中, 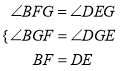 ,
,
∴△BFG≌△DGE(AAS),
∴GE=GF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是函数y=![]() 与函数y=
与函数y=![]() 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=![]() 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=![]() 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y=![]() 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习有理数运算时发现以下三个等式:(ab)2=a2b2,(ab)3=a3b3,(ab)4=a4b4.
(1)他把a=﹣2,b=3代入到第一个等式的左右两边验证:
因为,左=(﹣2×3)2=36,右=(﹣2)2×32=36,左=右,所以成立.
请你帮他把a=﹣2,b=3代入到后两个等式的左右两边验证是否成立;
(2)通过上述验证,请你猜想直接写出结果:(ab)365等于多少,归纳得出:(ab)n等于多少(n为正整数);
(3)请应用(2)中归出的结论计算:(﹣![]() )2017×112018
)2017×112018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正△ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求旋转角的度数;
(2)求点P与点P′之间的距离;
(3)求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )

A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解参加某校运动会的![]() 名运动员的年龄情况,从中抽取了
名运动员的年龄情况,从中抽取了![]() 名运动员的年龄,就这个问题,下面说法正确的是( )
名运动员的年龄,就这个问题,下面说法正确的是( )
A. ![]() 名运动员是总体 B. 每个运动员是个体
名运动员是总体 B. 每个运动员是个体
C. 抽取的![]() 名运动员是样本 D. 每个运动员的年龄是个体
名运动员是样本 D. 每个运动员的年龄是个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式 | 批发 | 零售 | 储藏后销售 |
售价(元/吨) | 3000 | 4500 | 5500 |
成本(元/吨) | 700 | 1000 | 1200 |
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的![]() .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
初中部 | a | 85 | b | s初中2 |
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com