
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处时,四边形AECF是矩形?并说出你的理由.

【答案】(1)OE=OF,证明见解析;(2)四边形BCFE不可能是菱形,理由见解析;(3)当点O运动到AC中点时,四边形AECF是矩形,理由见解析.
【解析】分析:(1)OE=OF,利用平行线的性质及角平分线的定义证得∠2=∠3,根据等腰三角形的性质可得OE=OC,同理可得OC=OF,即可得OE=OF;(2)四边形BCFE不可能是菱形,若四边形BCFE为菱形,则BF⊥EC,而由(1)可知FC⊥EC,这与在同一平面内过同一点有且只有一条直线与已知直线垂直相矛盾;(3)当点O运动到AC中点时,四边形AECF是矩形,先证明四边形AECF为平行四边形,再证明∠ECF=90°,根据有一个角为直角的平行四边形是矩形即可证得结论.
详解:
(1)OE=OF.
证明如下:
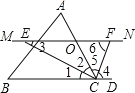
∵CE是∠ACB的平分线,
∴∠1=∠2.
∵MN∥BC,
∴∠1=∠3.
∴∠2=∠3.
∴OE=OC.
同理可证OC=OF.
∴OE=OF.
(2)四边形BCFE不可能是菱形,若四边形BCFE为菱形,则BF⊥EC,
而由(1)可知FC⊥EC,在平面内过同一点F不可能有两条直线同垂直于一条直线.
(3)当点O运动到AC中点时,四边形AECF是矩形.
理由如下:
∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴AECF为矩形


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?若能,请给出求解过程.
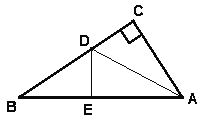
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) -26-(-15) (2)(+7)+(-4)-(-3)-14
(3)(-3)×![]() ÷(-2)×(-
÷(-2)×(-![]() ) (4)-(3-5)+32×(-3)
) (4)-(3-5)+32×(-3)
(5)(﹣![]() +
+![]() ﹣
﹣![]() +
+![]() )÷
)÷![]() (6)- 32 -(﹣2)2+1.
(6)- 32 -(﹣2)2+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( ) 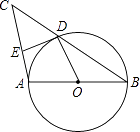
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
![]() 求收工时,检修小组在
求收工时,检修小组在![]() 地的哪个方向?距离
地的哪个方向?距离![]() 地多远?
地多远?
![]() 在第几次纪录时距
在第几次纪录时距![]() 地最远?
地最远?
![]() 若汽车行驶每千米耗油
若汽车行驶每千米耗油![]() 升,问从
升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) (2![]() -3
-3![]() )÷
)÷![]() ; (2) (
; (2) (![]() -
-![]() )2+2
)2+2![]() ×
×![]() ;
;
(3) ![]() ; (4) (
; (4) (![]() -2
-2![]() )×
)×![]() -4
-4![]() ;
;
(5)(![]() -1)(
-1)(![]() +1)-(-
+1)-(-![]() )-2+|1-
)-2+|1-![]() |-(π-2)0+
|-(π-2)0+![]() ;
;
(6)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com