
 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
| A.等于2 | B.等于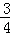 | C.等于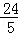 | D.无法确定 |
 a,
a, b),
b), a•
a• b=k,
b=k, 的图象上,
的图象上, 得,
得, ,
, ,
, (a﹣
(a﹣ )•b=3,
)•b=3, (a﹣
(a﹣ )•b=3,
)•b=3, )b=6,
)b=6,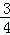 .
.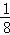 梯形DFAB=
梯形DFAB=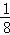 △BOC的面积=
△BOC的面积= ,
, k=
k= ,
,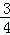 .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源:不详 题型:解答题
 的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ;
的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ; 的图象可由y=
的图象可由y= 的图象向 _________ 平移 _________ 个单位得到;y=
的图象向 _________ 平移 _________ 个单位得到;y= 的图象可由哪个反比例函数的图象经过怎样的变换得到;
的图象可由哪个反比例函数的图象经过怎样的变换得到; (ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?
(ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 关于y轴对称的函数的解析式为 .
关于y轴对称的函数的解析式为 . (k≠0)关于x轴对称的函数的解析式.
(k≠0)关于x轴对称的函数的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )
(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )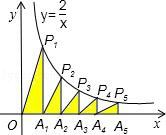
| A.2 | B.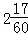 | C.3 | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为( )
的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为( )
 C.
C. D.不能确定
D.不能确定查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com