
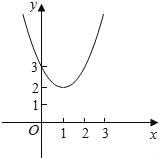
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
(1)求a,b,c的值;
(2)设二次函数y=k(2x+2)﹣(ax2+bx+c)
①若二次函数y=k(2x+2)﹣(ax2+bx+c)的图象与x轴的两个交点的横坐标x1,x2满足![]() ,求k的值;
,求k的值;
②请在二次函数y=ax2+bx+c与y=k(2x+2)﹣(ax2+bx+c)的图象上各找一个点M、N,且不论k为何值,这两个点始终关于x轴对称,求出点M、N的坐标(点M在点N的上方).
【答案】(1)a的值为1,b的值为﹣2,c的值为3;(2)①k=1或k=﹣5;②M(﹣1,6),N(﹣1,6).
【解析】
试题分析:(1)用待定系数法求出抛物线解析式中的字母a,b,c,(2)①先化简抛物线y=k(2x+2)﹣(ax2+bx+c)的解析式,再用根与系数的关系表示出x1+x2=2(k+1),x1x2=3﹣2k,最后用![]() 建立方程求解即可.②先设出点M的坐标,而点M,N关于x轴对称表示出点N的坐标,对称点的特点纵坐标互为相反数建立方程,得出(m+1)k=0,而不论k为何值,这两个点始终关于x轴对称,则有m+1=0,确定出m,最后得出点M,N的坐标.
建立方程求解即可.②先设出点M的坐标,而点M,N关于x轴对称表示出点N的坐标,对称点的特点纵坐标互为相反数建立方程,得出(m+1)k=0,而不论k为何值,这两个点始终关于x轴对称,则有m+1=0,确定出m,最后得出点M,N的坐标.
试题解析:(1)由已知得: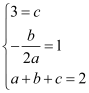 ,
,
解得: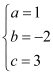 .
.
∴a的值为1,b的值为﹣2,c的值为3.
(2)①∵a=1,b=﹣2,c=3,
∴y=k(2x+2)﹣(ax2+bx+c)=﹣x2+2(k+1)x+2k﹣3,
∵二次函数y=k(2x+2)﹣(ax2+bx+c)的图象与x轴的两个交点的横坐标x1,x2,
∴x1+x2=2(k+1),x1x2=3﹣2k,
∴|x1﹣x2|=![]() ,
,
解得:k=1或k=﹣5;
②∵a=1,b=﹣2,c=3,
∴y=x2﹣2x+3和y=﹣x2+2(k+1)x+2k﹣3,
设M(m,m2﹣2m+3),
∵点M,N始终关于x轴对称,
∴N(m,﹣m2+2(k+1)m+2k﹣3)
m2﹣2m+3=﹣(﹣m2+2(k+1)m+2k﹣3),
∴(m+1)k=0
∵不论k为何值,点M,N始终关于x轴对称,
∴m+1=0,
∴m=﹣1,
∴M(﹣1,6),N(﹣1,6).


科目:初中数学 来源: 题型:
【题目】从2016年1月1日开始,北京市居民生活用气阶梯价格制度将正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按28元/m3收费,超过350立方米的部分按2.5元/m3收费.小冬一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况. 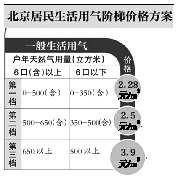
(1)如果他家2016年全年使用300立方米天然气,那么需要交多少元天然气费?
(2)如果他家2016年全年使用500立方米天然气,那么需要交多少元天然气费?
(3)如果他家2016年需要交1563元天然气费,他家2016年用了多少立方米天然气?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.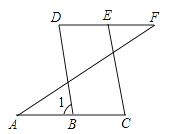
证明:∵∠A=∠F(已知)
∴AC∥ ,
∴∠D=∠1
又∵∠C=∠D(已知)
∴∠1=
∴BD∥CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.单项式 ![]() xy的系数是
xy的系数是 ![]() ,次数是1
,次数是1
B.单项式﹣ ![]() πa2b3的系数是﹣
πa2b3的系数是﹣ ![]() ,次数是6
,次数是6
C.单项式x2的系数是1,次数是2
D.多项式2x3﹣3x2y2+x﹣1叫三次四项式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077m,用科学记数法表示数的结果是( )
A.0.77×10﹣5m
B.0.77×10﹣6m
C.7.7×10﹣5m
D.7.7×10﹣6m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com