
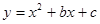 与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.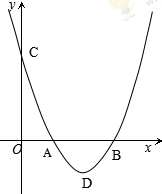
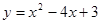 ;(2)(0,3),(2,-1);(3)
;(2)(0,3),(2,-1);(3)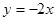 ;(4)(-1,2)或(-1.5,3)
;(4)(-1,2)或(-1.5,3)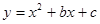 过点A(1,0)和B(3,0)根据待定系数法列方程组求解即可;
过点A(1,0)和B(3,0)根据待定系数法列方程组求解即可;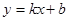 ,由点C、D的坐标根据待定系数法即可求得直线CD的解析式,再根据直线的平移规律:上加下减,即可求得结果;
,由点C、D的坐标根据待定系数法即可求得直线CD的解析式,再根据直线的平移规律:上加下减,即可求得结果;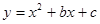 过点A(1,0)和B(3,0)
过点A(1,0)和B(3,0)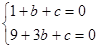 ,解得
,解得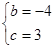
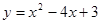 ;
;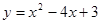 中,当x=0时,y=3,所以点C的坐标为(0,3)
中,当x=0时,y=3,所以点C的坐标为(0,3)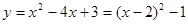 ,所以顶点D的坐标为(2,-1);
,所以顶点D的坐标为(2,-1);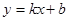
 ,解得
,解得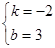
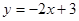 ,沿y轴向下平移3个单位长度后直线m的解析式为
,沿y轴向下平移3个单位长度后直线m的解析式为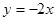 ;
;

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | … | | | | | | … |
| y | … | | | | | | … |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的顶点在x轴上,且与y轴交于A点. 直线
的顶点在x轴上,且与y轴交于A点. 直线 经过A、B两点,点B的坐标为(3,4).
经过A、B两点,点B的坐标为(3,4).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;
天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式; 元,试写出
元,试写出 与x之间的函数关系式;
与x之间的函数关系式; 元?
元?查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com