
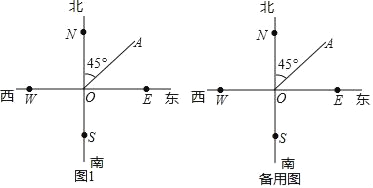
【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】“一带一路”国际合作高峰论坛于5月14日在北京开幕,学校在初三年级随机抽取了50名同学进行“一带一路”知识竞答,并将他们的竞答成绩绘制成如图的条形统计图,本次知识竞答成绩的中位数是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
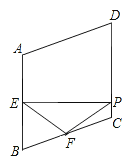
A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=35°,则∠A的度数为________;
(2)若∠DBC=α,求∠A的度数(用含α的代数式表示);
(3)已知120°<∠ABC<180°,若点F在线段AE上,连接BF,当△BFD为直角三角形时,求∠A与∠FBE的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校有一块长为(5a+b)米,宽为(3a+b)米的长方形空地,中间是边长(a﹣b)米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
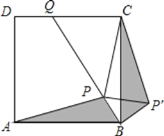
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为![]() ,1,2
,1,2![]() ,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1 , 使∠D1AC=60°;连接AC1 , 再以AC1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为 . 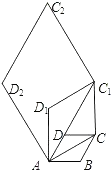
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

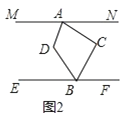
(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
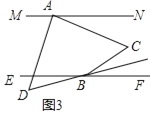
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.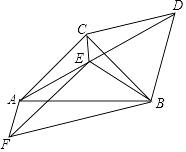
(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com