
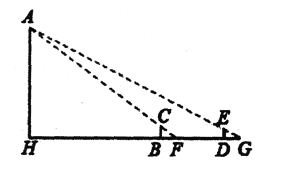
【题目】《海岛算经》第一个问题的大意是:如图,要测量海岛上一座山峰![]() 的高度
的高度![]() ,立两根高
,立两根高![]() 丈的标杆
丈的标杆![]() 和
和![]() ,两竿之间的距
,两竿之间的距![]() 步,
步,![]() 成一线,从
成一线,从![]() 处退行
处退行![]() 步到
步到![]() ,人的眼睛贴着地面观察
,人的眼睛贴着地面观察![]() 点,
点,![]() 三点成一线;从
三点成一线;从![]() 处退行
处退行![]() 步到
步到![]() ,从
,从![]() 观察
观察![]() 点,
点,![]() 三点也成一-线.试计算山峰的高度
三点也成一-线.试计算山峰的高度![]() 及
及![]() 的长. (这里
的长. (这里![]() 步
步![]() 尺,
尺,![]() 丈
丈![]() 尺,结果用丈表示) .怎样利用相似三角形求得线段
尺,结果用丈表示) .怎样利用相似三角形求得线段![]() 及
及![]() 的长呢?请你试一试!
的长呢?请你试一试!
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
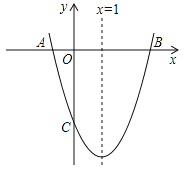
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若果∠1=∠2,那么添加下列任何一个条件:(1)![]() ,(2)
,(2)![]() ,(3)∠B=∠D,(4)∠C=∠AED, 其中能判定△ABC∽△ADE的个数为
,(3)∠B=∠D,(4)∠C=∠AED, 其中能判定△ABC∽△ADE的个数为

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
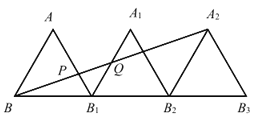
【题目】如图,![]() ,
,![]() ,△A2B2B3 是全等的等边三角形,点 B,B1,B2,B3 在同一条 直线上,连接 A2B 交 AB1 于点 P,交 A1B1 于点 Q,则 PB1∶QB1 的值为___.
,△A2B2B3 是全等的等边三角形,点 B,B1,B2,B3 在同一条 直线上,连接 A2B 交 AB1 于点 P,交 A1B1 于点 Q,则 PB1∶QB1 的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
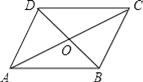
A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
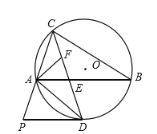
【题目】如图,圆![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是弧
是弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,则有下列结论:①点
,则有下列结论:①点![]() 是
是![]() 的重心;②
的重心;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,
, ![]() 是
是![]() 上的一动点,
上的一动点,![]() 是
是![]() 的中点,以
的中点,以![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 关于射线
关于射线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 、
、![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
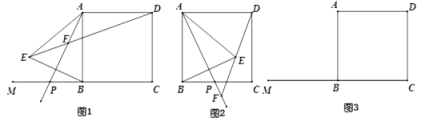
(1)如图1,当点![]() 在线段
在线段![]() 上,且
上,且![]() ,求
,求![]() 的度数;
的度数;
(2)小明在解题时发现:当点![]() 在线段
在线段![]() 上时,线段
上时,线段![]() ,
,![]() ,
,![]() 之间满足
之间满足![]() ,那么你认为当点
,那么你认为当点![]() 在线段
在线段![]() 上时(如图2),他的结论是否还成立?若成立,请证明,若不成立,请说明理由;
上时(如图2),他的结论是否还成立?若成立,请证明,若不成立,请说明理由;
(3)如图3,点![]() 在
在![]() 上,且
上,且![]() ,当点
,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,直接写出点
时,直接写出点![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
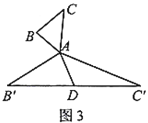
【题目】定义:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )并延长一倍得到
)并延长一倍得到![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 并延长一倍得到
并延长一倍得到![]() ,连接
,连接![]() .当
.当![]() 时,称
时,称![]() 是
是![]() 的“倍旋三角形”,
的“倍旋三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“倍旋中线”.
的“倍旋中线”.
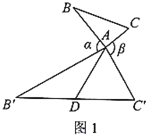
特例感知:
(1)如图1,当![]() ,
,![]() 时,则“倍旋中线”
时,则“倍旋中线”![]() 长为______;如图2,当
长为______;如图2,当![]() 为等边三角形时,“倍旋中线”
为等边三角形时,“倍旋中线”![]() 与
与![]() 的数量关系为______;
的数量关系为______;
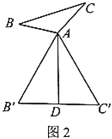
猜想论证:
(2)在图3中,当![]() 为任意三角形时,猜想“倍旋中线”
为任意三角形时,猜想“倍旋中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
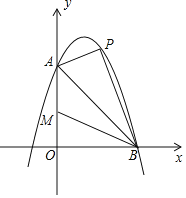
【题目】如图,已知抛物线![]() 与y轴交于点
与y轴交于点![]() ,与x轴交于点
,与x轴交于点![]() ,点P是线段AB上方抛物线上的一个动点.
,点P是线段AB上方抛物线上的一个动点.
![]() 求这条抛物线的表达式及其顶点坐标;
求这条抛物线的表达式及其顶点坐标;
![]() 当点P移动到抛物线的什么位置时,使得
当点P移动到抛物线的什么位置时,使得![]() ,求出此时点P的坐标;
,求出此时点P的坐标;
![]() 当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动;与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止
当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动;与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止![]() 当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?
当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com