
【题目】下列命题:(1)两直线平行,内错角相等;(2)如果m是无理数,那么m是无限小数;(3)64的立方根是8;(4)同旁内角相等,两直线平行;(5)如果a是实数,那么![]() 是无理数.(6)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(7)直线外一点到这条直线的垂线段,叫做该点到直线的距离;(8)过一点作已知直线的平行线,有且只有一条.其中是真命题的有 ( )
是无理数.(6)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(7)直线外一点到这条直线的垂线段,叫做该点到直线的距离;(8)过一点作已知直线的平行线,有且只有一条.其中是真命题的有 ( )
A. 0个B. 1个C. 2个D. 3个
【答案】D
【解析】
利用平行线的性质、无理数的定义、立方根的知识及实数的有关知识分别判断后即可确定正确的选项.
解:(1)两直线平行,内错角相等,正确;
(2)如果m是无理数,那么m是无限小数,正确;
(3)64的立方根是4,故错误;
(4)同旁内角互补,两直线平行,故错误;
(5)如果a是实数,那么![]() 是无理数,错误.
是无理数,错误.
(6)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,强调了在平面内,正确;
(7)直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离,不是指点到直线的垂线段的本身,而是指垂线段的长度,故错误;
(8)过直线外一点作已知直线的平行线,有且只有一条,故错误.
故选:D.


科目:初中数学 来源: 题型:
【题目】“一般的,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.﹣﹣苏科版《数学》九年级(下册)P21”参考上述教材中的话,判断方程x2﹣2x= ![]() ﹣2实数根的情况是( )
﹣2实数根的情况是( )
A.有三个实数根
B.有两个实数根
C.有一个实数根
D.无实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )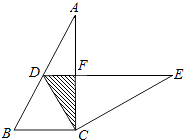
A.30,2
B.60,2
C.60, ![]()
D.60, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,正方形ABFG和FCDE的顶点均和小正方形的顶点重合.
(1)建立平面直角坐标系,使得B,C的坐标分别为(0,0),(4,0),并写出点A的坐标;
(2)直接写出正方形FCDE的边长;
(3)连接EG,直接比较三角形BCF和三角形GEF的面积大小 (用“大于”,“小于”,“等于”作答)

查看答案和解析>>
科目:初中数学 来源: 题型:
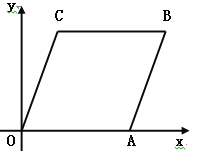
【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面![]() 倒下到
倒下到![]() 的位置,连接
的位置,连接![]() ,设
,设![]() 、
、![]() 、
、![]() ,请利用四边形
,请利用四边形![]() 的面积验证勾股定理.
的面积验证勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,∠2+∠3=180,请说明AB与DE平行的理由.
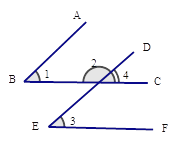
解:将∠2的邻补角记作∠4,则
∠2+∠4=180°( )
因为∠2+∠3=180°( )
所以∠3=∠4( )
因为______________(已知)
所以∠1=∠4( )
所以AB//DE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com