
分析 根据三角形数得到x1=1,x2=3=1+2,x3=6=1+2+3,x4=10=1+2+3+4,x5=15=1+2+3+4+5,即三角形数为从1到它的顺号数之间所有整数的和,即xn=1+2+3+…+n=$\frac{n(n+1)}{2}$、xn+1=$\frac{(n+1)(n+2)}{2}$,然后计算xn+xn+1可得.
解答 解:∵x1=1,
x2═3=1+2,
x3=6=1+2+3,
x4═10=1+2+3+4,
x5═15=1+2+3+4+5,
…
∴xn=1+2+3+…+n=$\frac{n(n+1)}{2}$,xn+1=$\frac{(n+1)(n+2)}{2}$,
则xn+xn+1=$\frac{n(n+1)}{2}$+$\frac{(n+1)(n+2)}{2}$=(n+1)2,
故答案为:(n+1)2.
点评 本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 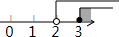 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com