
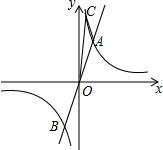
 如图,已知直线y=3x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.
如图,已知直线y=3x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.分析 探究:首先利用正比例函数解析式计算出A点坐标,再把A点坐标代入反比例函数y=$\frac{k}{x}$,可得反比例函数解析式;分别过点C,A作CD⊥x轴,AE⊥x轴,再利用反比例函数解析式计算出点C的坐标,根据反比例函数解析式计算出S△CDO=S△AEO=$\frac{1}{2}$|k|,再用S△AOC=S四边形COEA-S△AOE=S四边形COEA-S△COD=S梯形CDEA,即可算出答案;
拓展:由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即为5.可根据双曲线的解析式设出P点的坐标,然后参照上面三角形面积的求法表示出△POA的面积,由于△POA的面积为5,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
解答 解:探究:∵点A在直线y=3x上,且点A的横坐标为2,
∴y=3×2=6,
∴A(2,6),
∵点A(2,6)在双曲线y=$\frac{k}{x}$上,
∴6=$\frac{k}{2}$,
解得:k=12.
即双曲线的解析式为y=$\frac{12}{x}$.
如图1,分别过点C,A作CD⊥x轴,AE⊥x轴,垂足分别为点D,E.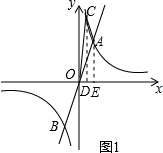 ∵点C在双曲线y=$\frac{12}{x}$上,点C的纵坐标为12,
∵点C在双曲线y=$\frac{12}{x}$上,点C的纵坐标为12,
∴12=$\frac{12}{x}$,
解得:x=1,
即点C的坐标为(1,12),
∵点A,C都在双曲线y=$\frac{12}{x}$上,
∴S△AOE=S△COD=$\frac{1}{2}$×12=6,
∴S△AOC=S四边形COEA-S△AOE=S四边形COEA-S△COD=S梯形CDEA,
∴S△AOC=$\frac{1}{2}$(AE+CD)•DE=$\frac{1}{2}$(6+12)×1=9;
拓展:∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,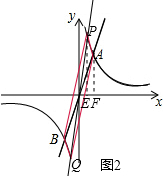 ∴四边形APBQ是平行四边形,
∴四边形APBQ是平行四边形,
∴S△POA=$\frac{1}{4}$S平行四边形APBQ=$\frac{1}{4}$×20=5,
设点P的横坐标为m(m>0且m≠2),得P(m,$\frac{12}{m}$),
过点P、A分别作x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=6,
若0<m<2,如图2,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=5,
∴$\frac{1}{2}$(6+$\frac{12}{m}$)•(2-m)=5,
∴m=$\frac{4}{3}$,m=-3(舍去),
∴P($\frac{4}{3}$,9);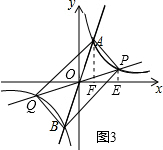 若m>2,如图3,
若m>2,如图3,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=5,
∴$\frac{1}{2}$(6+$\frac{12}{m}$)•(m-2)=5,
解得m=3,m=-$\frac{4}{3}$(舍去),
∴P(3,4).
所以点P的坐标是:P($\frac{4}{3}$,9)或P(3,4).
故答案为($\frac{4}{3}$,9)或(3,4).
点评 本题考查了反比例解析式的确定和性质、图形的面积求法、反比例函数与一次函数的交点等知识及综合应用知识、解决问题的能力.难点是不规则图形的面积通常转化为规则图形的面积的和差来求解.


科目:初中数学 来源: 题型:选择题
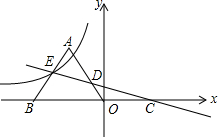 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )| A. | -$\frac{6}{7}$ | B. | -$\sqrt{3}$ | C. | -3 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
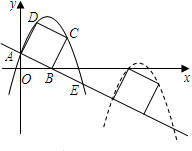 如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com