
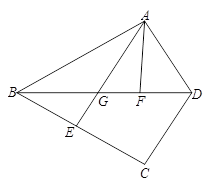
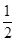 ∠BAF,AF=
∠BAF,AF=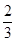 AD,试探究线段FM和FN之间的数量关系,并证明你的结论.
AD,试探究线段FM和FN之间的数量关系,并证明你的结论.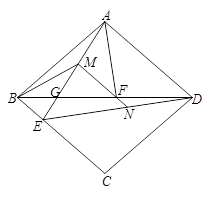
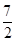 FN.
FN.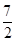 FN.理由如下:由△AFG∽△BFA,易得∠AGF=∠BAF,所以结合已知条件和图形得到∠MBG=∠BMG.易证△AGF∽△DGA,则对应边成比例:
FN.理由如下:由△AFG∽△BFA,易得∠AGF=∠BAF,所以结合已知条件和图形得到∠MBG=∠BMG.易证△AGF∽△DGA,则对应边成比例: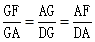 .即
.即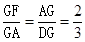 .设GF=2a(a>0),AG=3a,则GD=
.设GF=2a(a>0),AG=3a,则GD=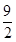 a,FD=
a,FD=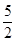 a;利用平行线(BE∥AD)截线段成比例易得
a;利用平行线(BE∥AD)截线段成比例易得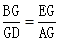 ,则
,则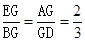 .设EG=2k(k>0),所以BG=MG=3k.如图2,过点F作FQ∥ED交AE于点Q.则又由FQ∥ED,易证得
.设EG=2k(k>0),所以BG=MG=3k.如图2,过点F作FQ∥ED交AE于点Q.则又由FQ∥ED,易证得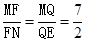 ,所以FM=
,所以FM=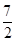 FN.
FN.
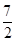 FN
FN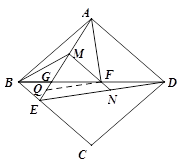
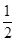 ∠BAF,∴∠MBF=
∠BAF,∴∠MBF=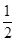 ∠AGF
∠AGF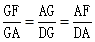
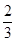 AD
AD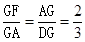
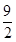 a,∴FD=DG-GF=
a,∴FD=DG-GF=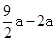 =
=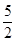 a
a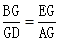 .∴
.∴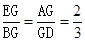 ,
,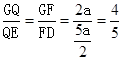 .∴
.∴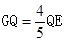 ,∴GQ=
,∴GQ=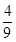 EG=
EG=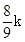
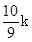 ∴MQ=MG+GQ=3k+
∴MQ=MG+GQ=3k+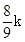 =
=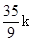
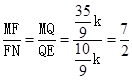 .
.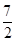 FN.
FN.

科目:初中数学 来源:不详 题型:填空题
 ,则CD的长为_________________.
,则CD的长为_________________.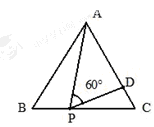
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com