
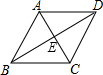
 如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )
如图,要想证明平行四边形ABCD是菱形,下列条件中不能添加的是( )| A. | ∠ABD=∠ADB | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
分析 根据菱形的判定(①有一组邻边相等的平行四边形是菱形,②四条边都相等的四边形是菱形,③对角线互相垂直的平行四边形是菱形)判断即可.
解答 解:A、∵∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,故本选项不合题意;
B、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故本选项不合题意;
C、四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故本选项不合题意;
D、根据四边形ABCD是平行四边形和AC=BD,得出四边形ABCD是矩形,不能推出四边形是菱形,故本选项符合题意;
故选:D.
点评 本题考查了菱形的判定定理的应用,注意:菱形的判定定理有①有一组邻边相等的平行四边形是菱形,②四条边都相等的四边形是菱形,③对角线互相垂直的平行四边形是菱形.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
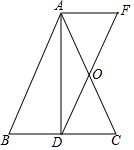 如图,已知在△ABC中,D为BC上一点,连接AD,过点A作AF∥BC,过点D作DF∥AB,AF与DF交于点F,DF与AC交于点O,若AO=OC.
如图,已知在△ABC中,D为BC上一点,连接AD,过点A作AF∥BC,过点D作DF∥AB,AF与DF交于点F,DF与AC交于点O,若AO=OC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{75}$ | B. | $5\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $7\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com