练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （8分）已知：如图，AC与BD相交于点O，∠ABC=∠DCB，AB=DC，

    求证：∠OBC=∠OCB。

    见解析 【解析】试题分析：本题考查了全等三角形的判定与性质，根据SAS可判定△ABC≌△DCB，然后根据全等三角形的额对应角相等可证∠OBC=∠OCB. 证明：在△ABC和△DCB中 ∴△ABC≌△DCB ∴OBC=∠OCB
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：填空题

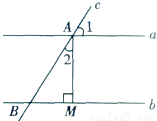
    如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为点M，若∠l=58°，则∠2= ___________ .

    32° 【解析】根据“在同一平面内，垂直于两条平行线中的一条直线，那么必定垂直于另一条直线”推知AM⊥a；然后由平角是180°、∠1=58°来求∠2的度数即可． 【解析】 ∵直线a∥b，AM⊥b， ∴AM⊥a（在同一平面内，垂直于两条平行线中的一条，那么必定垂直于另一条）； ∴∠2=180°-90°-∠1； ∵∠1=58°， ∴∠2=32°． 故答案是：...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：单选题

    有三张正面分别写有数字－1，1，2的卡片，它们背面完全相同，现将这三张卡片背面朝上洗匀后随机抽取一张，以其正面数字作为a的值，然后再从剩余的两张卡片随机抽一张，以其正面的数字作为b的值，则点(a，b)在第二象限的概率为(　　)

    A. B. C. D.

    B 【解析】根据题意画出树状图 一共有6种情况,在第二象限的点有2个,所以,,故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：单选题

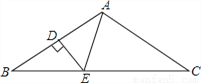
    如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（ ）

    A. 80° B. 60° C. 50° D. 40°

    D 【解析】首先利用三角形的内角和定理和等腰三角形的性质∠B，利用线段垂直平分线的性质易得AE=BE，∠BAE=∠B． 【解析】 ∵AB=AC，∠BAC=100°，∴∠B=∠C=（180°﹣100°）÷2=40°，∵DE是AB的垂直平分线，∴AE=BE，∴∠BAE=∠B=40°， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：单选题

    如图，在△ABC中，∠C＝40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1－∠2的度数是（ ）

    A. 40° B. 80° C. 90° D. 140°

    B 【解析】 由题意得：∠C=∠D， ∵∠1=∠C+∠3，∠3=∠2+∠D， ∴∠1=∠2+∠C+∠D=∠2+2∠C， ∴∠1－∠2=2∠C=80°. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：解答题

    （每小题5分，共10分）计算：

    （1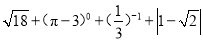） （2）

    （1）+3；（2）-2 【解析】试题分析：（1）第一项根据二次根式的性质化简，第二项非零数的零次方等于1，第三项负整数指数幂等于这个数正整数幂的倒数，第四项负数的绝对值等于它的相反数；（2）根据平方差公式计算. （1） （2） =1-3 =2.

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：填空题

    不等式 的解集是 _____________。

    x>-1 【解析】, +3, .

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

    一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长．

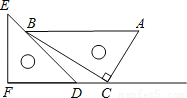
    15﹣5． 【解析】 试题分析：过点B作BM⊥FD于点M，根据题意可求出BC的长度，然后在△EFD中可求出∠EDF=45°，进而可得出答案． 【解析】 过点B作BM⊥FD于点M， 在△ACB中，∠ACB=90°，∠A=60°，AC=10， ∴∠ABC=30°，BC=AC×tan60°=10， ∵AB∥CF， ∴BM=BC×sin30°=10×=5， ...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：单选题

    一元二次方程x2﹣6x﹣5=0配方可变形为（　　）

    A. （x﹣3）2=14 B. （x﹣3）2=4 C. （x+3）2=14 D. （x+3）2=4

    A 【解析】试题分析：x2﹣6x﹣5=0，把方程的常数项移到右边得，x2﹣6x=5，方程两边都加上32得，x2﹣6x+9=5+9，所以（x﹣3）2=14，故答案选C.

    查看答案和解析>>

    同步练习册答案