
【题目】如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=53°,且DE=2.4米,求匾额悬挂的高度AB的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ).
).
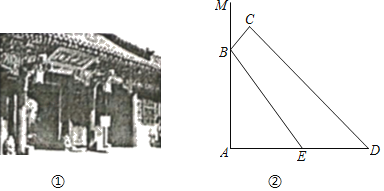
【答案】匾额悬挂的高度是4米.
【解析】
过C作CF⊥AM于F,过C作CH⊥AD于H,根据直角三角形的解法解答即可.
过C作CF⊥AM于F,过C作CH⊥AD于H,则四边形AHCF是矩形,所以AF=CH,CF=AH.

在Rt△BCF中,BC=1,∠CBF=37°.
BF=BCcos37°=0.8,CF=BCsin37°=0.6,
在Rt△BAE中,∠BEA=53°,所以AE=![]() AB,
AB,
在Rt△CDH中,∠CDH=45°,
∴CH=DH=FA=0.8+AB,
∴AD=AH+DH=0.6+0.8+AB=1.4+AB,
∵AD=AE+DE=![]() AB+2.4,
AB+2.4,
∴1.4+AB=![]() AB+2.4,
AB+2.4,
AB=4,
答:匾额悬挂的高度是4米.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,过点A作AD⊥BO交BO的廷长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中AB=BC,将△ABC绕点C顺时针旋转α角时,点A的对应点A′恰好落在AB边上,则∠A′CB=_____(用含α的式子来表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
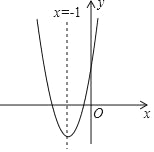
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=10,一个三角形的直角顶点E是边AB上的一动点,一直角边过点D,另一直角边与BC交于F,若AE=x,BF=y,则y关于x的函数关系的图象大致为( )
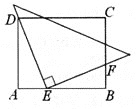
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
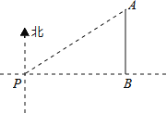
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家出台了《城市生活垃圾分类标志》根据国家制定的统一标志,生活垃圾被重新划分为四类,它们分别是可回收垃圾、不可回收垃圾、有害垃圾和其他垃圾.可回收垃圾指适宜回收和资源利用的垃圾,包括纸类、塑料、玻璃、织物和瓶罐等,用蓝色垃圾容器收集;不可回收垃圾指除可回收垃圾之外的垃圾,包括果皮、菜叶、剩饭等,用绿色垃圾容器收集;有害垃圾指含有害物质,需要特殊安全处理的垃圾,包括电池、灯管和日用化学品等,用红色垃圾容器收集;其他垃圾指分类以外的垃圾,用灰色垃圾容器收集.一天,小林把垃圾分装在四个袋中,可他在投放时,只把餐余垃圾正确投放进了不可回收垃圾桶中,其余三袋垃圾不小心都放错了位置(都没有正确放入对应垃圾箱内).请你用树状图或列表的方法说明把剩余三个袋子都放错位置的概率是多少?(在画树状图或列表时,“可回收垃圾”用“![]() ”表示,“不可回收垃圾”用“
”表示,“不可回收垃圾”用“![]() ”表示,“有害垃圾”用“
”表示,“有害垃圾”用“![]() ”表示,“其他垃圾”用“
”表示,“其他垃圾”用“![]() ”表示)
”表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=6,∠B=75°,将△ABC沿AC边折叠得到△AB′C,B′C交AD于E,∠B′AE=45°,则点A到BC的距离为( )

A.2![]() B.3
B.3![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com