
【题目】如图,在等边△ABC中,BD=CE,连接AD、BE交于点F.
(1)求∠AFE的度数;
(2)求证:ACDF=BDBF;
(3)连接FC,若CF⊥AD时,求证:BD=![]() DC.
DC.
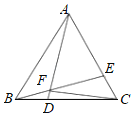
【答案】(1)60°;(2)证明见解析;(3)证明见解析
【解析】
(1)证明△ABD≌△BCE(SAS),得出∠BAD=∠CBE,则∠BFD=∠AFE=∠ABC=60°;
(2)证明△ADB∽△BDF,得出![]() ,由AB=AC可得出结论;
,由AB=AC可得出结论;
(3)延长BE至H,使FH=AF,连接AH,CH,证明△BAF≌△CAH(SAS),得出∠ABF=∠ACH,CH=BF,可证明AF∥CH,得出![]() ,进而即可得出答案.
,进而即可得出答案.
解:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
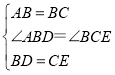 ,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠ABC,
∴∠BFD=∠AFE=∠ABC=60°;
(2)证明:由(1)知∠BAD=∠DBF,
又∵∠ADB=∠BDF,
∴△ADB∽△BDF,
∴![]() ,
,
又AB=AC,
∴![]() ,
,
∴ACDF=BDBF;
(3)证明:延长BE至H,使FH=AF,连接AH,CH,
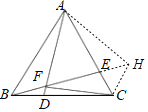
由(1)知∠AFE=60°,∠BAD=∠CBE,
∴△AFH是等边三角形,
∴∠FAH=60°,AF=AH,
∴∠BAC=∠FAH=60°,
∴∠BAC﹣∠CAD=∠FAH﹣∠CAD,
即∠BAF=∠CAH,
在△BAF和△CAH中,
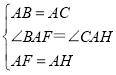 ,
,
∴△BAF≌△CAH(SAS),
∴∠ABF=∠ACH,CH=BF,
又∵∠ABC=∠BAC,∠BAD=∠CBE,
∴∠ABC﹣∠CBE=∠BAC﹣∠BAD,
即∠ABF=∠CAF,
∴∠ACH=∠CAF,
∴AF∥CH,
∵∠AFC=90°,∠AFE=60°,
∴CF⊥CH,∠CFH=30°,
∴FH=2CH,
∴FH=2BF,
∵FD∥CH,
∴![]() ,
,
∴BD=![]() DC.
DC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
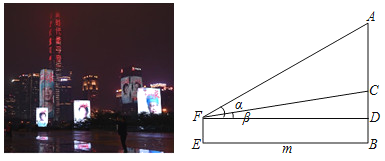
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两张完全重合的矩形纸片,将其中一张绕点![]() 顺时针旋转
顺时针旋转![]() 后得到矩形
后得到矩形![]() (如图1),连接
(如图1),连接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)试探究线段![]() 与线段
与线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)把![]() 与
与![]() 剪去,将
剪去,将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,边
,边![]() 交
交![]() 于点
于点![]() (如图2),设旋转角为
(如图2),设旋转角为![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数;
的度数;
(3)若将![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如图3),
(如图3),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求平移的距离.
时,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的内接三角形,且
的内接三角形,且![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() .
.
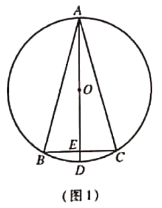
![]() 如图1 ,求证:
如图1 ,求证:![]() ;
;
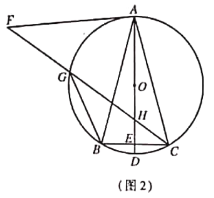
![]() 如图2,将线段
如图2,将线段![]() 绕点
绕点![]() 顺时针旋转得到线段
顺时针旋转得到线段![]() ,旋转角为
,旋转角为![]() 连接
连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证: ![]() ;
;
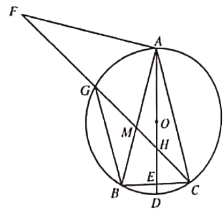
![]() 如图3,在(2)的条件下,当
如图3,在(2)的条件下,当![]() 时,
时,![]() 交
交![]() 于点
于点![]() 若
若![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简:![]() +
+![]() +…+
+…+![]() .
.
为了能找到复杂计算问题的结果,我们往往会通过将该问题分解,试图找寻算式中每个式子是否存在某种共同规律,然后借助这个规律将问题转化为可以解决的简单问题.下面我们尝试着用这个思路来解决上面的问题.请你按照这个思路继续进行下去,并把相应横线上的空格补充完整.
(分析问题)第1个加数:![]() =
=![]() ﹣
﹣![]() ;
;
第2个加数:![]() =
=![]() ﹣
﹣![]() ;
;
第3个加数:![]() =
=![]() ﹣
﹣![]() ;
;
第4个加数: =![]() ﹣
﹣![]() ;
;
(总结规律)第n个加数: = ﹣ .
(解决问题)请你利用上面找到的规律,继续化简下面的问题.(结果只需化简,无需求出最后得数)![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
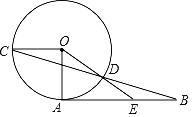
【题目】如图,AB是⊙O的切线,OA,OC是⊙O的半径,且OC∥AB,连接BC交⊙O于点D,点D恰为BC的中点,连接OD并延长,交AB于点E.
(1)求∠B的度数;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
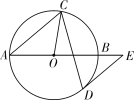
A.65°B.30°C.25°D.20°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com