
���� ��1����������ó�a��b�ķ����飬�ⷽ���鼴�ɣ�
��2���ٸ�������=����������-�����ܳɱ������ɵó������
���̵�Ҫ����������y��0���ó�����ʽ���ⲻ��ʽ���ɣ�
��� �⣺��1����������ã�
$\left\{\begin{array}{l}{a+b=40}\\{40b-50a=700}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=10}\\{b=30}\end{array}\right.$��
��a��b��ֵ�ֱ�Ϊ10��30��
��2���ٸ�������ã�y=60x+35��40-x��-��10��50+30��40����
��y=25x-300��
���̵�Ҫ����������y��0��
��25x-300��0��
��ã�x��12��
�𣺵�x��ֵ����Ϊ12ʱ���̵�Ų��������
���� ���⿼���˶�Ԫһ�η������Ӧ�á�һ�κ�����Ӧ�ã���������ó�������ϵ�г��������ó�������ϵʽ���ɲ��ȹ�ϵ�ó�����ʽ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У���E��F�ֱ���AB��CD���е㣬����DE��BF���ֱ�ȡDE��BF���е�M��N������AM��CN��MN����AB=2$\sqrt{2}$��BC=2$\sqrt{3}$����ͼ����Ӱ���ֵ������
��ͼ������ABCD�У���E��F�ֱ���AB��CD���е㣬����DE��BF���ֱ�ȡDE��BF���е�M��N������AM��CN��MN����AB=2$\sqrt{2}$��BC=2$\sqrt{3}$����ͼ����Ӱ���ֵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���۵�����ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪�ۺ�AE=5$\sqrt{5}$cm����$\frac{EC}{FC}$=$\frac{3}{4}$��
��ͼ���۵�����ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪�ۺ�AE=5$\sqrt{5}$cm����$\frac{EC}{FC}$=$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
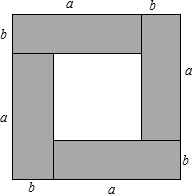 ��ѧ�����һ����Ҫ����ѧ˼�룬�������ַ������ǿ��Խ��������ѧ֪ʶ���ֱ���Ҿ��пɲ����ԣ�������ѧ��Ĵ�����ʽ���кܶ����ͨ����ʾ����ͼ������ķ��������Ƶ�����֤��������ȫƽ����ʽ���������ǽ������Ƶ�̽����
��ѧ�����һ����Ҫ����ѧ˼�룬�������ַ������ǿ��Խ��������ѧ֪ʶ���ֱ���Ҿ��пɲ����ԣ�������ѧ��Ĵ�����ʽ���кܶ����ͨ����ʾ����ͼ������ķ��������Ƶ�����֤��������ȫƽ����ʽ���������ǽ������Ƶ�̽�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��BD��DE��D��CE��DE��E��AΪ�߶�DE��һ�㣬��AB=AC��AD=CE��
��ͼ��BD��DE��D��CE��DE��E��AΪ�߶�DE��һ�㣬��AB=AC��AD=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com