
【题目】探究归纳题: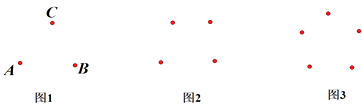
(1)试验分析:
如图1,经过A点与B、C两点分别作直线,可以作条;同样,经过B点与A、C两点分别作直线,可以作条;经过C点与A、B两点分别作直线,可以作条.
通过以上分析和总结,图1共有条直线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有条直线;
图3共有条直线;
(3)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在同一直线上,经过其中两点共有条直线.(用含n的式子表示)
(4)解决问题:
中职篮(CBA)2017——2018赛季作出重大改革,比赛队伍数扩充为20支,截止2017年12月21日赛程过半,即每两队之间都赛了一场,请你帮助计算一下一共进行了多少场比赛?
【答案】
(1)2;2;2;3
(2)6;10
(3)![]()
(4)解: 当n=20时, ![]() =
= ![]() (场).
(场).
故一共进行了190场比赛
【解析】解:(1)2;2;2;3;(2)6;10;(3) ![]() (1)根据两点确定一条直线,图1中,过点A的直线有两条,过点B的直线有两条 ,过点C的直线有两条 ,一共有直线6条,但在计算的过程中,每条直线都计算了两次,故一共有直线
(1)根据两点确定一条直线,图1中,过点A的直线有两条,过点B的直线有两条 ,过点C的直线有两条 ,一共有直线6条,但在计算的过程中,每条直线都计算了两次,故一共有直线![]() =3条 ;
=3条 ;
(2)(1)根据两点确定一条直线,图2中,过其中一点的直线有3条,而图中共有4个点,,一共有直线12条,但在计算的过程中,每条直线都计算了两次,故一共有直线![]() =6条 ;图3中,过其中一点的直线有4条,而图中共有5个点,,一共有直线20条,但在计算的过程中,每条直线都计算了两次,故一共有直线
=6条 ;图3中,过其中一点的直线有4条,而图中共有5个点,,一共有直线20条,但在计算的过程中,每条直线都计算了两次,故一共有直线![]() =10条 ;
=10条 ;
(3)根据上面找到的规律,如果平面上有n(n≥3)个点,且每3个点均不在同一直线上,经过其中1点共有(n-1)条,而图中共有n个点,一共有直线n(n-1)条,但在计算的过程中,每条直线都计算了两次,故一共有直线![]() 条 ;
条 ;
(4)中职篮篮球比赛场次问题,其实就是刚才这类问题,只需把n=20代入![]() 计算即可得出答案。
计算即可得出答案。


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: 
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】与 ![]() 在平
在平![]() 面直角坐标系中的位置如图.
面直角坐标系中的位置如图.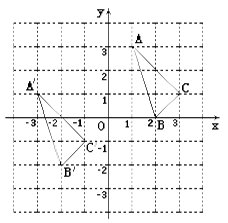
(1)分别写出下列各点的坐标:![]() ;
; ![]() ;
; ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:
经过怎样的平移得到:
.
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的
内的
对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论: ①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有( )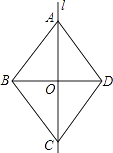
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
A.AB=A′B′
B.BC∥B′C′
C.直线l⊥BB′
D.∠A′=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a。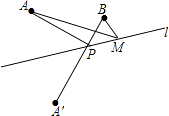
(1)求AP+PB。
(2)若点M是直线l上异于点P的任意一点,求证:AM+MB>AP+PB。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B,P在一条直线上,则下列等式中,能判断点P是线段AB中点个数有 ( )
①AP=BP;②.BP= ![]() AB;③AB=2AP;④AP+PB=AB.
AB;③AB=2AP;④AP+PB=AB.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com