
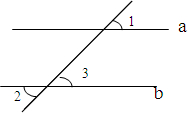
 填空:如图,已知∠1=∠2,求证:a∥b
填空:如图,已知∠1=∠2,求证:a∥b科目:初中数学 来源: 题型:解答题
 如图,活动衣帽架由三个相同菱形组成,利用四边形的不稳定性,调整菱形的内角A,使衣帽架拉伸或收缩,若菱形的边长等于10cm,∠A=120°,则AB=10cm.AD=30cm.
如图,活动衣帽架由三个相同菱形组成,利用四边形的不稳定性,调整菱形的内角A,使衣帽架拉伸或收缩,若菱形的边长等于10cm,∠A=120°,则AB=10cm.AD=30cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠BAE大39°.设∠BAE和∠B′AD的度数分别为x,y,那么x,y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠BAE大39°.设∠BAE和∠B′AD的度数分别为x,y,那么x,y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}{y-x=39}\\{y+x=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=39}\\{y+2x=90}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-x=39}\\{y=2x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=39}\\{y+2x=90}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )
如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )| A. | 2cm | B. | 3cm | C. | $\sqrt{3}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )
如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )| A. | 四边形AFCE是平行四边形 | B. | 四边形AFCE是菱形 | ||
| C. | 四边形ABCF是等腰梯形 | D. | 四边形AECD是等腰梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com