【题目】如图,已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O.下列结论：①∠DOC=90°, ②OC=OE， ③tan∠OCD =
，④
中，正确的有（ ）
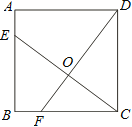
A.1个B.2个C.3个D.4个
【答案】C
【解析】
∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°．
∵AE=BF=1，∴BE=CF=4－1=3．
在△EBC和△FCD中，∵BC=CD，∠B=∠DCF，BE=CF，∴△EBC≌△FCD（SAS）．
∴∠CFD=∠BEC．∴∠BCE+∠BEC=∠BCE+∠CFD=90°．
∴∠DOC=90°．故①正确．
如图，连接DE
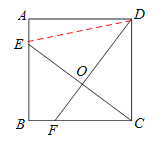
若OC=OE，∵DF⊥EC，∴CD=DE．
∵CD=AD＜DE（矛盾），故②错误．
∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC．
∴tan∠OCD=tan∠DFC=
．故③正确．
∵△EBC≌△FCD，∴S△EBC=S△FCD．
∴S△EBC－S△FOC=S△FCD－S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．
科目：初中数学 来源： 题型：
【题目】2016年4月23日是我国第一个“全民阅读日”某校开展了“建设书香校园，捐赠有益图书”活动．我们在参加活动的所有班级中，随机抽取了一个班，已知这个班是八年级5班，全班共50名学生．现将该班捐赠图书情况的统计结果，绘制成如下两幅不完整的统计图．
请你根据以上信息，解答下列问题：
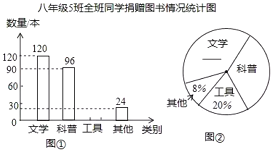
（1）补全上面的条形统计图和扇形统计图；
（2）求八年级5班平均每人捐赠了多少本书？
（3）若该校八年级共有800名学生，请你估算这个年级学生共可捐赠多少本书？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，BC是⊙O的切线，D是⊙O上的一点，且AD//CO．
（1）求证：△ADB∽△OBC；
（2）若AB=2，BC=
，求AD的长．（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在ABCD中，∠D=30°，AB＜AD．
（1）在AD边上求作一点P，使点P到边AB，BC的距离相等；(要求：尺规作图，不写作法，保留作图痕迹)
（2）在（1）的条件下，连接BP，若AB=2，求△ABP的面积．
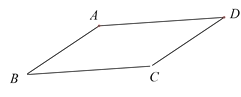
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某网店专售一款电动牙刷，其成本为20元/支，销售中发现，该商品每天的销售量y(支）与销售单价x(元/支）之间存在如图所示的关系．
(1)求y与x之间的函数关系式．
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎（简称“新冠肺炎”）疫情，该网店店主决定从每天获得的利润中抽出200元捐献给武汉，为了保证捐款后每天剩余利润不低于550元，如何确定这款电动牙刷的销售单价？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
，
分别与
相切于点
和点
，点
为弧
上一点，连接
并延长交于点
，
为弧
上的一点，连接
交
于点
，连接
，且
．
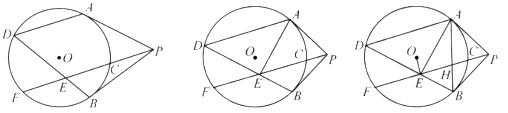
（1）如图1，求证：
；
（2）如图2，连接
，若
，求证：
平分
；
（3）如图3，在（2）的条件下，连接交于点
，连接
，
，
，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）问题发现
如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：
①
的值为 ；
②∠AMB的度数为 ．
（2）类比探究
如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；
（3）拓展延伸
在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=
，请直接写出当点C与点M重合时AC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
