
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,点D为BC的中点,点E,F分别在直线AB,AC上运动,且始终保持AE=CF.
(1)如图①,若点E,F分别在线段AB,AC上,求证:DE=DF且DE⊥DF; 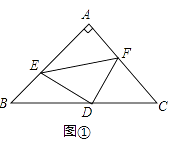
(2)如图②,若点E、F分别在线段AB,CA的延长线上,(1)中的结论是否依然成立?说明理由. 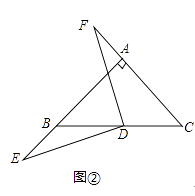
【答案】
(1)解:如图①,连接AD,
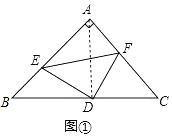
∵∠BAC=90°,AB=AC,D为BC中点,
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
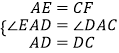 ,
,
∴△AED≌△CFD(SAS),
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF+∠ADF=90°,
∴∠ADE+∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF
(2)解:若点E,F分别在线段AB,CA的延长线上,(1)中的结论依然成立,如图②,
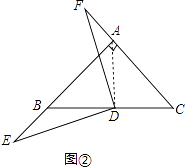
理由:∵∠BAC=90° AB=AC,D为BC中点
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
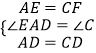 ,
,
∴△AED≌△CFD(SAS);
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF﹣∠ADF=90°,
∴∠ADE﹣∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF
【解析】(1)利用等腰直角三角形的性质得出AD=BD=DC,进而证明△AED≌△CFD,利用全等三角形的性质得出DE=DF,∠ADE=∠CDF进而得出△DEF为等腰直角三角形;(2)若点E、F分别在线段AB,CA的延长线上,(1)中的结论依然成立,首先利用已知得出AD=BD=DC,进而利用全等三角形的判定得出△AED≌△CFD.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,∠AOC=∠BOC,点P在OC上,
求证: .
请你补全已知和求证
(2)并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队一位新兵进行射击训练,连续射靶5次,命中的环数分别是0,2,5,2,7.这组数据的中位数与众数分别是( )
A.2,5
B.2,2
C.5,7
D.2,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数m,n,定义一种运算“※”:m※n=m2﹣mn﹣3.下列说法错误的是( )
A. 0※1=﹣3 B. 方程x※2=0的根为x1=﹣1,x2=3
C. 不等式组![]() 无解 D. 函数y=x※(﹣2)的顶点坐标是(1,﹣4)
无解 D. 函数y=x※(﹣2)的顶点坐标是(1,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°. 因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号)
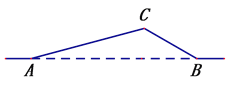
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com