
 如图,已知菱形ABCD的两条对角线长分别为12和16,M、N分别是边BC、CD的中点,P是对角线BD上一动点,则PM+PN的最小值为10.
如图,已知菱形ABCD的两条对角线长分别为12和16,M、N分别是边BC、CD的中点,P是对角线BD上一动点,则PM+PN的最小值为10. 分析 要求PM+PN的最小值,PM、PN不能直接求,可考虑通过作辅助线转化PN、PM的值,从而找出其最小值求解.
解答 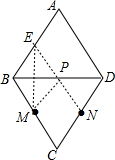 解:如图:
解:如图:
作ME⊥BD交AB于E,连接EN,
则EN就是PM+PN的最小值,
∵四边形ABCD是菱形,
∴AB=CD,
∵M、N分别是边BC、CD的中点,
∴BE=CN,
∴四边形EBCN是平行四边形,
∴EN=BC,
而由题意可知,可得BC=$\sqrt{(\frac{12}{2})^{2}+(\frac{16}{2})^{2}}$=10,
∴EN=10,
∴PM+PN的最小值为10.
故答案为:10.
点评 考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用.综合运用这些知识是解决本题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售渠道 | 每日销量 (吨) | 每吨所获纯 利润(元) |
| 省城批发 | 4 | 1200 |
| 本地零售 | 1 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,现有一个圆心角为90°,半径为12cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的底面半径为( )
如图,现有一个圆心角为90°,半径为12cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的底面半径为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | πcm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com