
���� ��1�������оٷ�����չʾ����6�ֿ��ܵĽ����
��3�������б���չʾ���ҳ˳������н����Ȼ��������dz����ϵȳ��ĸ��ʣ��ٱȽϸ��ʵĴ�С��
��� �⣺��1���������������Ⱥ�˳����6�ֿ��ܣ�
���ϡ��С��£������ϡ��¡��У������С��ϡ��£������С��¡��ϣ������¡��С��ϣ������¡��ϡ��У���
��2���б����£�
| ˳�� | �� | �� |
| �ϡ��С��� | �� | �� |
| �ϡ��¡��� | �� | �� |
| �С��ϡ��� | �� | �� |
| �С��¡��� | �� | �� |
| �¡��ϡ��� | �� | �� |
| �¡��С��� | �� | �� |
���� ���⿼�����б�������״ͼ����ͨ���б�������״ͼ��չʾ���еȿ��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ����¼�A��B�ĸ��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪EC=BF����A=��D���ִ�����6��������
��ͼ����֪EC=BF����A=��D���ִ�����6��������| A�� | �ڢۢܢ� | B�� | �ۢܢݢ� | C�� | �٢ۢܢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-��x-4��2+9 | B�� | y=-x2+9 | C�� | y=-��x-5��2+8 | D�� | y=-x2+8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{12}$ | B�� | $\sqrt{{a}^{2}b}$ | C�� | $\sqrt{0.5}$ | D�� | $\sqrt{x{\;}^{2}+1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 6 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
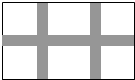 ѧУ��������С����������dz�20��15�ij����Σ�Ϊ�˱��ڹ�������Ҫ���м俪��һ�����ݵȿ���С������ͼ����Ҫʹ��ֲ���Ϊ252ƽ���ף���С���Ŀ���
ѧУ��������С����������dz�20��15�ij����Σ�Ϊ�˱��ڹ�������Ҫ���м俪��һ�����ݵȿ���С������ͼ����Ҫʹ��ֲ���Ϊ252ƽ���ף���С���Ŀ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
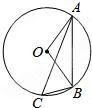 ��ͼ����O�ǡ�ABC�����Բ����֪��ABO=50�㣬���ACB�Ĵ�СΪ��������
��ͼ����O�ǡ�ABC�����Բ����֪��ABO=50�㣬���ACB�Ĵ�СΪ��������| A�� | 40�� | B�� | 30�� | C�� | 45�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com