
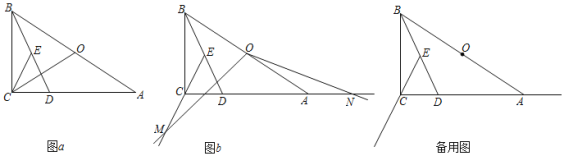
【题目】在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系: ;
(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①如图b,猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).
【答案】(1)∠ECO=∠OAC;(2)①OM=ON,理由见解析,②EM的值为m+![]() m或
m或![]() m﹣
m﹣![]() m
m
【解析】
(1)结论:∠ECO=∠OAC.理由直角三角形斜边中线定理,三角形的中位线定理解决问题即可.
(2)①只要证明△COM≌△AON(ASA),即可解决问题.
②分两种情形:如图3﹣1中,当点N在CA的延长线上时,如图3﹣2中,当点N在线段AC上时,作OH⊥AC于H.分别求解即可解决问题.
解:(1)结论:∠ECO=∠OAC.
理由:如图1中,连接OE.

∵∠BCD=90°,BE=ED,BO=OA,
∵CE=ED=EB=![]() BD,CO=OA=OB,
BD,CO=OA=OB,
∴∠OCA=∠A,
∵BE=ED,BO=OA,
∴OE∥AD,OE=![]() AD,
AD,
∴CE=EO.
∴∠EOC=∠OCA=∠ECO,
∴∠ECO=∠OAC.
故答案为:∠OCE=∠OAC.
(2)如图2中,
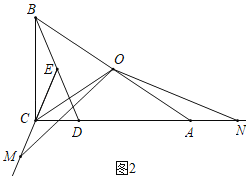
∵OC=OA,DA=DB,
∴∠A=∠OCA=∠ABD,
∴∠COA=∠ADB,
∵∠MON=∠ADB,
∴∠AOC=∠MON,
∴∠COM=∠AON,
∵∠ECO=∠OAC,
∴∠MCO=∠NAO,
∵OC=OA,
∴△COM≌△AON(ASA),
∴OM=ON.
②如图3﹣1中,当点N在CA的延长线上时,

∵∠CAB=30°=∠OAN+∠ANO,∠AON=15°,
∴∠AON=∠ANO=15°,
∴OA=AN=m,
∵△OCM≌△OAN,
∴CM=AN=m,
在Rt△BCD中,∵BC=m,∠CDB=60°,
∴BD=![]() m,
m,
∵BE=ED,
∴CE=![]() BD=
BD=![]() m,
m,
∴EM=CM+CE=m+![]() m.
m.
如图3﹣2中,当点N在线段AC上时,作OH⊥AC于H.

∵∠AON=15°,∠CAB=30°,
∴∠ONH=15°+30°=45°,
∴OH=HN=![]() m,
m,
∵AH=![]() m,
m,
∴CM=AN=![]() m﹣
m﹣![]() m,
m,
∵EC=![]() m,
m,
∴EM=EC﹣CM=![]() m﹣(
m﹣(![]() m﹣
m﹣![]() m)=
m)=![]() m﹣
m﹣![]() m,
m,
综上所述,满足条件的EM的值为m+![]() m或
m或![]() m﹣
m﹣![]() m.
m.


科目:初中数学 来源: 题型:
【题目】如图:已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
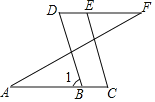
解:∵∠A=∠F(已知)
∴AC∥DF(______)
∴∠D=∠1(______)
又∵∠C=∠D(已知)
∴∠1=______
∴BD∥CE(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(图①为实景侧视图,图②为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为1.4 m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安装工人已确定支架AB高为25 cm,求支架CD的高.(结果精确到1 cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
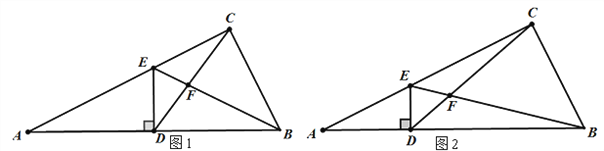
【题目】如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=![]() ,则
,则![]() =_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若
=_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若![]() ,tanA=
,tanA=![]() ,则
,则![]() =____.
=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=_____度;
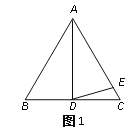
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=_______度;
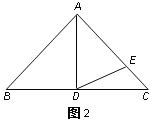
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________.
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
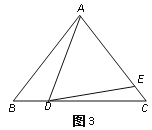
查看答案和解析>>
科目:初中数学 来源: 题型:
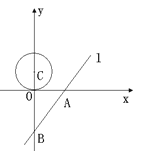
【题目】如图,已知直线![]() 的解析式是
的解析式是![]() ,并且与
,并且与![]() 轴、
轴、![]() 轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着
轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着![]() 轴向下运动,当⊙C与直线
轴向下运动,当⊙C与直线![]() 相切时,则该圆运动的时间为( )
相切时,则该圆运动的时间为( )
A. 3秒或6秒 B. 6秒 C. 3秒 D. 6秒或16秒
查看答案和解析>>
科目:初中数学 来源: 题型:
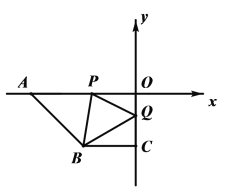
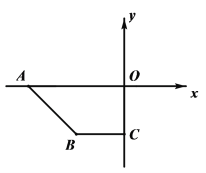
【题目】如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足![]() ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
(1)直接写出点B的坐标,AO和BC位置关系是;
(2)当P、Q分别是线段AO,OC上时,连接PB,QB,使![]() ,求出点P的坐标;
,求出点P的坐标;
(3)在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图l,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com