
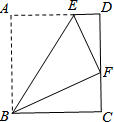
 如图,在矩形ABCD中,E是AD上一点.将矩形ABCD沿BE翻折,使得点F落在CD上.
如图,在矩形ABCD中,E是AD上一点.将矩形ABCD沿BE翻折,使得点F落在CD上.分析 (1)根据两角对应相等的两个三角形全等即可判断.
(2)由BF=2CF推出,∠FBC=30°即可解决问题.
(3)首先证明△ABF、△GMN是等边三角形,设AB=a,AG=x,想办法列出关于a、x的方程,即可解决问题.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=∠D=90°,
∴∠BFC+∠FBC=90°,
∵矩形ABCD沿BE翻折后,点F落在CD上,
∴∠A=∠EFB=90°,
∴∠EFD+∠BFC=90°
∴∠EFD=∠FBC,
又∵∠C=∠D,
∴△DEF∽△CFB,
(2)∵△BEF是由△BEA翻折得到,
∴BF=AB=CD,
∵DF=FC,
∴BF=2CF,
∴∠FBC=30°,
在RT△BCF中,∵∠C=90°,∠FBC=30°,
∴BC=$\sqrt{3}$CF,
∴AB=$\frac{2\sqrt{3}}{3}$BC.
(3)解:在(2)中有CF=DF,
又∵四边形ABCD是矩形,
∴AD=BC,∠C=∠D=90°,
在△ADF和△BCF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠D=∠C}\\{DF=FC}\end{array}\right.$,
∴△ADF≌△BCF.
∴AF=BF.
由翻折可知:AB=BF.
∴AF=AB=BF,
∴△ABF是等边三角形.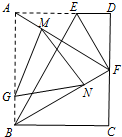
∵△GMN∽△ABF,
∴△GMN是等边三角形,
∴∠GMN=60°,MG=MN,
∵∠FMG=∠MAG+∠AGM=∠GMN+∠NMF,
∴∠NMF=∠AGM,
在△AGM和△FMN中,
$\left\{\begin{array}{l}{∠MAG=∠MFN}\\{∠AGM=∠NMF}\\{MG=MN}\end{array}\right.$
∴△AGM≌△FMN,同理△AGM≌△BNG,
∵S△GMN=$\frac{1}{2}$S△ABF,
∴S△AGM=$\frac{1}{6}$S△ABF
设AB=a,
∴BC=$\frac{\sqrt{3}}{2}$a,
∴S△ABF=$\frac{\sqrt{3}}{4}$a2,
∴S△AGM=$\frac{\sqrt{3}}{24}$a2,
设AG=x,则BG=AM=a-x.
∴M到AB的距离为$\frac{\sqrt{3}}{2}$(a-x),
∴S△AGM=$\frac{\sqrt{3}}{4}$x (a-x),
∴$\frac{\sqrt{3}}{24}$a2=$\frac{\sqrt{3}}{4}$x (a-x),
整理得到:6x2-6xa+a2=0,
∴x=$\frac{3±\sqrt{3}}{6}$a,
∴$\frac{AG}{AB}$=$\frac{3±\sqrt{3}}{6}$.
点评 本题考查矩形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是熟练掌握这些知识的应用,学会把问题转化为方程解决,体现了数形结合的思想,属于中考压轴题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
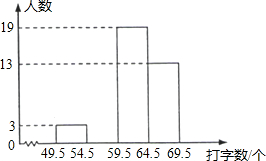 初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:| 打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
| 人数 | 1 | 2 | 8 | 11 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com