
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.

(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)求当![]() 时,
时,![]() 的值,当
的值,当![]() 时,
时,![]() 的值;
的值;
(3)过点![]() 作直线
作直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且使
,且使![]() ,求
,求![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】某商场用3000元购进某种商品,由于销售状况良好,商场又用9000元购进这种商品,但这次的进价比第一次的进价提高了20%,购进商品比第一次的2倍还多300千克,如果商场按每千克9元出售.
求:(1)该种商品第一次的进价是每千克多少元?
(2)超市销售完这种商品共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
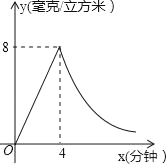
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB至点F,使BF=BD连接AF.
(1)求证:AF=CD.
(2)若CE平分∠ACB交AB于点E,试猜想AC,AF,AE三条线段之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线C1:![]() 与x轴的一个交点为A(-1,0),另一个交点为B,与
与x轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴的交点为C(0,-3),其顶点为D.
轴的交点为C(0,-3),其顶点为D.
(1)求抛物线C1的解析式;
(2)如图1,将△OBC沿![]() 轴向右平移m个单位长度(0﹤
轴向右平移m个单位长度(0﹤![]() ≤
≤![]() )得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
)得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
(3)如图2,将抛物线C1平移,使其顶点为原点O,得到抛物线C2.若直线![]() 与抛物线C2交于S、T两点,点
与抛物线C2交于S、T两点,点![]() 是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.
是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.


查看答案和解析>>
科目:初中数学 来源: 题型:
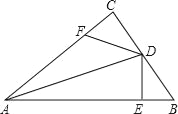
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的反比例函数,且点A(3,5)在这个函数的图象上.
(1)求y与x之间的函数关系式;
(2)当点B(-5,m)也在这个反比例函数的图象上时,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com