
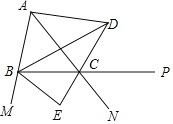
【题目】如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°.其中正确的结论有_____.(填序号)
【答案】①②③④
【解析】
根据角平分线的定义、三角形的内角和定理、三角形的外角的性质、平行线的判定一一判断即可.
解:①设点A,B在直线MF上,
∵BD、CD分别平分△ABC的内角∠ABC、外角∠ACP,
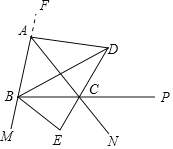
∴AD平分△ABC的外角∠FAC,
∴∠FAD=∠DAC,
∵∠FAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠FAD=∠ABC,
∴AD∥BC,故①正确.
②∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC,
∴∠DBE=∠DBC+∠EBC=![]() ∠ABC+
∠ABC+![]() ∠MBC=
∠MBC=![]() ×180°=90°,
×180°=90°,
∴EB⊥DB,故②正确,
③∵∠DCP=∠BDC+∠CBD,2∠DCP=∠BAC+2∠DBC,
∴2(∠BDC+∠CBD)=∠BAC+2∠DBC,
∴∠BDC=![]() ∠BAC,
∠BAC,
∵∠BAC+2∠ACB=180°,
∴![]() ∠BAC+∠ACB=90°,
∠BAC+∠ACB=90°,
∴∠BDC+∠ACB=90°,故③正确,
④∵∠BEC=180°﹣![]() (∠MBC+∠NCB)=180°﹣
(∠MBC+∠NCB)=180°﹣![]() (∠BAC+∠ACB+∠BAC+∠ABC)=180°﹣
(∠BAC+∠ACB+∠BAC+∠ABC)=180°﹣![]() (180°+∠BAC),
(180°+∠BAC),
∴∠BEC=90°﹣![]() ∠BAC,
∠BAC,
∴∠BAC+2∠BEC=180°,故④正确,
故答案为:①②③④.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,BC=3,AB=4,![]() ,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C作射线CM且满足∠ACM=∠ABC.
(1)判断CM与⊙O的位置关系,并证明;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2,2,3,4四个数中随机取两个数,第一个作为个位上的数字,第二个作为十位上的数字,组成一个两位数,则这个两位数是2的倍数的概率是 ( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b经过点A(0,3)和点B(4,a),且点B在正比例函数y=![]() x的图象上.
x的图象上.
(1)求a的值.
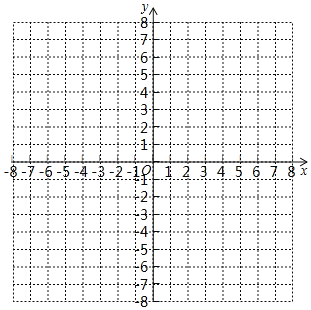
(2)求k和b的值,并在给定的坐标系内画出这条直线.
(3)如果点C(![]()
![]() ,y1)和点D(﹣
,y1)和点D(﹣![]() ,y2)都在这条直线上,请比较y1和y2的大小.
,y2)都在这条直线上,请比较y1和y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com