
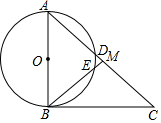
 如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.分析 (1)利用直角三角形斜边上的中线性质得MA=MB,则∠A=∠MBA,再利用圆内接四边形的性质证明∠MDE=∠MED,于是得到MD=ME;
(2)先证明△OAD和△OBE为等边三角形,再证明四边形DOEM为平行四边形,然后加上OD=OE可判断四边形ODME是菱形.
解答 解:(1)在Rt△ABC中,点M是AC的中点,
∴MA=MB,
∴∠A=∠MBA;
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
而∠ADE+∠MDE=180°,
∴∠MDE=∠MBA;
同理可得∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME;
(2)当∠A=60°时,
则∠ABM=60°,
∴△OAD和△OBE为等边三角形,
∴∠BOE=60°,
∴∠BOE=∠A,
∴OE∥AC,
同理可得OD∥BM,
∴四边形DOEM为平行四边形,
而OD=OE,
∴四边形ODME是菱形.
故答案为60°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了菱形的判定.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
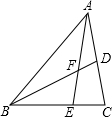 如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).
如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,其中点B坐标为(4,3).
如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,其中点B坐标为(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{3}y$ | D. | $-\frac{1}{3}y$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
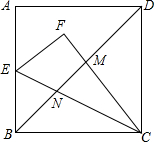 在正方形ABCD中,AD=4.点E是线段AB的中点,连接CE,将△BCE沿CE翻折,使点B落在点F处,对角线BD与CF,CE分别相交于点M,N,则MN的长是$\frac{20}{21}\sqrt{2}$..
在正方形ABCD中,AD=4.点E是线段AB的中点,连接CE,将△BCE沿CE翻折,使点B落在点F处,对角线BD与CF,CE分别相交于点M,N,则MN的长是$\frac{20}{21}\sqrt{2}$..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com