
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
【答案】(1)见解析;(2) 201,207,255
【解析】
试题(1)先设出两位自然数的十位数字,表示出这个两位自然数,和轮换两位自然数即可;
(2)先表示出三位自然数和轮换三位自然数,再根据能被5整除,得出b的可能值,进而用4整除,得出c的可能值,最后用能被3整除即可.
试题解析:
(1)设两位自然数的十位数字为x,则个位数字为2x,
∴这个两位自然数是10x+2x=12x,
∴这个两位自然数是12x能被6整除,
∵依次轮换个位数字得到的两位自然数为10×2x+x=21x
∴轮换个位数字得到的两位自然数为21x能被7整除,
∴一个两位自然数的个位数字是十位数字的2倍,这个两位自然数一定是“轮换数”.
(2)∵三位自然数![]() 是3的一个“轮换数”,且a=2,
是3的一个“轮换数”,且a=2,
∴100a+10b+c能被3整除,
即:10b+c+200能被3整除,
第一次轮换得到的三位自然数是100b+10c+a能被4整除,
即100b+10c+2能被4整除,
第二次轮换得到的三位自然数是100c+10a+b能被5整除,
即100c+b+20能被5整除,
∵100c+b+20能被5整除,
∴b+20的个位数字不是0,便是5,
∴b=0或b=5,
当b=0时,
∵100b+10c+2能被4整除,
∴10c+2能被4整除,
∴c只能是1,3,5,7,9;
∴这个三位自然数可能是为201,203,205,207,209,
而203,205,209不能被3整除,
∴这个三位自然数为201,207,
当b=5时,∵100b+10c+2能被4整除,
∴10c+502能被4整除,
∴c只能是1,5,7,9;
∴这个三位自然数可能是为251,255,257,259,
而251,257,259不能被3整除,
∴这个三位自然数为255,
即这个三位自然数为201,207,255.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的边BC位于直线l上,AC=![]() ,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).
,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC=5,AB=1,AB⊥BC,射线CM⊥BC,动点P在线段BC上(不与点B,C重合),过点P作DP⊥AP交射线CM于点D,连接AD.
(1)如图1,若BP=4,判断△ADP的形状,并加以证明.
(2)如图2,若BP=1,作点C关于直线DP的对称点C′,连接AC′.
①依题意补全图2;
②请直接写出线段AC′的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.

(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:如图(1)和图(2)中,点P是平面内一点,如果![]() =2或
=2或![]() =
=![]() ,称点P是线段AB的强弱点.
,称点P是线段AB的强弱点.
(1)如图2,在Rt△APB中,∠APB=90°,∠A=30°,问:点B是否是线段AP的强弱点?请说明理由;
(2)如图3,在Rt△ABC中,∠ACB=90°,B是线段AC的强弱点(BA>BC),BD是Rt△ABC的角平分线,求证:点D是线段AC上的强弱点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两块面积相同的小麦试验田,播种时第一块使用原品种,第二块使用新品种,分别收获小麦9000kg和15000kg.已知第一块试验田每公顷的产量比第二块试验田每公顷的产量少3000kg,分别求这两块试验田每公顷的产量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需130元;购买5个A奖品和4个B奖品共需230元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共40个,且A奖品的数量不少于B奖品数量的![]() .购买预算金不超过920元,请问学校有几种购买方案.
.购买预算金不超过920元,请问学校有几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
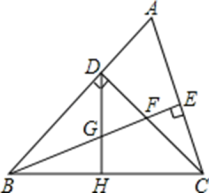
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com