
直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连结
,连结![]() ,抛物线
,抛物线![]() 从点
从点![]() 沿
沿![]() 方向平移,与直线
方向平移,与直线![]() 交于点
交于点![]() ,顶点
,顶点![]() 到
到![]() 点时停止移动.
点时停止移动.
(1)求线段![]() 所在直线的函数解析式;(2)设抛物线顶点
所在直线的函数解析式;(2)设抛物线顶点![]() 的横坐标为
的横坐标为![]() ,①用
,①用![]() 的代数式表示点
的代数式表示点![]() 的坐标;②当
的坐标;②当![]() 为何值时,线段
为何值时,线段![]() 最短;
最短;
(3)当线段![]() 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点![]() ,使△
,使△![]() 的面积与△
的面积与△![]() 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点![]() 的坐标;若,不存在,请说明理由.
的坐标;若,不存在,请说明理由.

解 (1)设![]() 所在直线的函数解析式为
所在直线的函数解析式为![]() ,
,
∵![]() (2,4), ∴
(2,4), ∴![]() ,
, ![]() ,
,
∴![]() 所在直线的函数解析式为
所在直线的函数解析式为![]()
(2)①∵顶点M的横坐标为![]() ,且在线段
,且在线段![]() 上移动,
上移动,
∴![]() (0≤
(0≤![]() ≤2). ∴顶点
≤2). ∴顶点![]() 的坐标为(
的坐标为(![]() ,
,![]() ).
).
∴抛物线函数解析式为![]() .
.
∴当![]() 时,
时,![]()
![]() (0≤
(0≤![]() ≤2).
≤2).
∴点![]() 的坐标是(2,
的坐标是(2,![]() )
)
② ∵![]() =
=![]() =
=![]() , 又∵0≤
, 又∵0≤![]() ≤2,
≤2,
∴当![]() 时,PB最短.
时,PB最短.
(3)当线段![]() 最短时,此时抛物线的解析式为
最短时,此时抛物线的解析式为![]()
假设在抛物线上存在点![]() ,使
,使![]() .
.
设点![]() 的坐标为(
的坐标为(![]() ,
,![]() ).
).
①当点![]() 落在直线
落在直线![]() 的下方时,过
的下方时,过![]() 作直线
作直线![]() //
//![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() , ∴
, ∴![]() 点的坐标是(0,
点的坐标是(0,![]() ).
).
 ∵点
∵点![]() 的坐标是(2,3),∴直线
的坐标是(2,3),∴直线![]() 的函数解析式为
的函数解析式为![]() .
.
∵![]() ,∴点
,∴点![]() 落在直线
落在直线![]() 上.
上.
∴![]() =
=![]() .
.
解得![]() ,即点
,即点![]() (2,3).
(2,3).
∴点![]() 与点
与点![]() 重合.
重合.
∴此时抛物线上不存在点![]() ,使△
,使△![]() 与△
与△![]() 的
的
面积相等.
②当点![]() 落在直线
落在直线![]() 的上方时,
的上方时,
作点![]() 关于点
关于点![]() 的对称称点
的对称称点![]() ,过
,过![]() 作直线
作直线![]() //
//![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.![]() 的坐标分别是(0,1),(2,5),
的坐标分别是(0,1),(2,5),
∴直线![]() 函数解析式为
函数解析式为![]() .
.
∵![]() ,∴点
,∴点![]() 落在直线
落在直线![]() 上.
上.
∴![]() =
=![]() .
.
解得:![]() ,
,![]() .
.
代入![]() ,得
,得![]() ,
,![]() .
.
综上所述,抛物线上存在点![]() ,
,![]()
使△![]() 与△
与△![]() 的面积相等.
的面积相等.


科目:初中数学 来源: 题型:
| 4 |
| 5 |
| 24 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 x2+
x2+ x-4与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
x-4与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME. 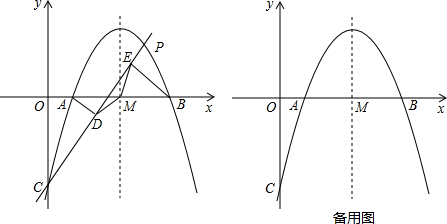
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
如图,抛物线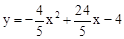 与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
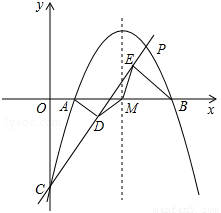
(1)求点A,B的坐标(直接写出结果),并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点P的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴下方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能,求此时点P的坐标(直接写出结果);若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年辽宁省大连市中考数学试卷(解析版) 题型:解答题
 x2+
x2+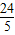 x-4与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
x-4与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME. 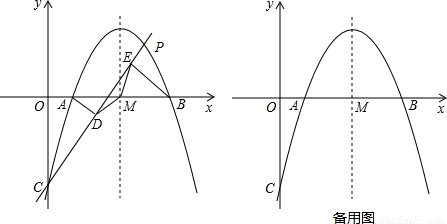
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com