
分析 连接DF,设AD和BF交于G点,根据三角形的中位线性质可得AB=2DF,DF∥AB,然后根据平行线分线段成比例定理从而得到AG=2GD,BG=2GF,同理证得CG′=2G′E,AG′=2G′D,即可证得结论.
解答 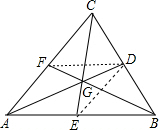 证明:如图,连接DF,设AD和BF交于G点,
证明:如图,连接DF,设AD和BF交于G点,
∵AD、BF、CE是△ABC的中线
∴DF是△ABC的中位线,
∴AB=2DF,DF∥AB,
∴$\frac{AG}{GD}$=$\frac{BG}{GF}$=$\frac{AB}{DF}$=$\frac{2}{1}$,
∴AG=2GD,BG=2GF,
设AD和CE交于G′,
同理可得:CG′=2G′E,AG′=2G′D,
即G和G′重合,
所以,三角形的三条中线AD、BF、CE交于一点,且被该交点分成的两段长度之比为2:1.
点评 本题考查了三角形的重心定理的证明,作辅助线构造成三角形的中位线和相似三角形是解题的关键,也是本题的难点.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是一施工队建房时挖地基的平面图,按标准应为长方形,挖完后,技术人员经测量发现AB=DC=12m,AD=BC=5m,AC=14m,请你帮忙检验一下挖的是否合格?
如图,是一施工队建房时挖地基的平面图,按标准应为长方形,挖完后,技术人员经测量发现AB=DC=12m,AD=BC=5m,AC=14m,请你帮忙检验一下挖的是否合格?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com