
【题目】综合与探究:
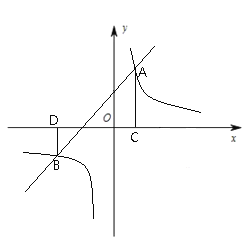
如图所示,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)求![]() ,
,![]() 的值及反比例函数的函数表达式;
的值及反比例函数的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请求出此时点
,请求出此时点![]() 的坐标;
的坐标;
(3)小颖在探索中发现:在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形.请你直接写出点
为顶角的等腰三角形.请你直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]()
【解析】
(1)利用点在直线上,将点的坐标代入直线解析式中求解即可求出a,b,最后用待定系数法求出反比例函数解析式;
(2)设点![]() ,用三角形的面积公式得到
,用三角形的面积公式得到![]() 求解即可得出结论;
求解即可得出结论;
(3)设出点M坐标,表示出MA2=(m-1)2+9,AB2=32,根据等腰三角形的性质建立方程求解即可得出结论.
解:(1)∵直线![]() 与反比例函数
与反比例函数![]() 的图象交与
的图象交与![]() ,
,![]() 两点
两点
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∵点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() .
.
∴反比例函数的函数表达式为![]() .
.
(2)设点![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∵![]()
∴![]() .
.
解得:![]() ,
,
∴![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
(3)设出点M坐标为(m,0),
∴MA2=(m-1)2+9,AB2=(1+3)2+(3+1)2=32,
∵![]() 是以
是以![]() 为顶角的等腰三角形
为顶角的等腰三角形
∴AM=AB,
故(m-1)2+9=32
解得m=![]() 或m=
或m=![]() (舍去)
(舍去)
∴![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙M的半径为4,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k≠0)的图象经过点A(1,2)和B(2,n),
(k≠0)的图象经过点A(1,2)和B(2,n),
(1)以原点O为位似中心画出△A1B1O,使![]() =
=![]() ;
;
(2)在y轴上是否存在点P,使得PA+PB的值最小?若存在,求出P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整)
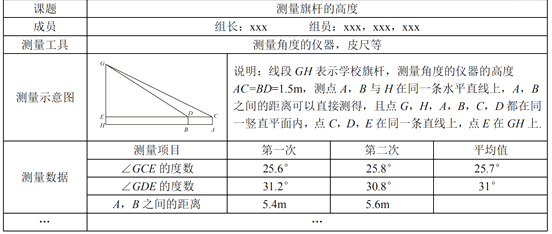

任务一:两次测量A,B之间的距离的平均值是 m.
任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
任务三:该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.

(1)如图1、用含x的代数式表示△MNP的面积S;
(2)如图2、⊙O与直线BC相切D点,求x的值为多少?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,![]() 的平分线交图形G于点D,连接AD,CD.
的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE![]() BA,垂足为E,作DF
BA,垂足为E,作DF![]() BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
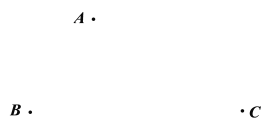
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2m+1)x﹣3m.
(1)若m=2,写出该函数的表达式,并求出函数图象的对称轴.
(2)已知点P(m,y1),Q(m+4,y2)在该函数图象上,试比较y1,y2的大小.
(3)对于此函数,在﹣1≤x≤1的范围内至少有x值使得y≥0,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
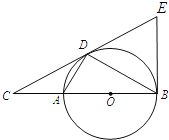
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=4,tan∠ABD=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,以点
,以点![]() 为圆心经过
为圆心经过![]() 、
、![]() 两点画圆分别与
两点画圆分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() (异于点
(异于点![]() ).
).
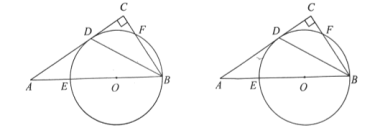
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 恰好是
恰好是![]() 的中点,求
的中点,求![]() 的长;
的长;
(3)若![]() 的长为
的长为![]() .
.
①求![]() 的半径长;
的半径长;
②点![]() 关于
关于![]() 轴对称后得到点
轴对称后得到点![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com