
【题目】在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,如图24-1-4-12.此时,甲自己直接射门好,还是迅速将球传给乙,让乙射门好?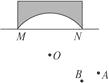
【答案】考虑过M、N及A、B中任一点作圆,这里不妨过M、N、B作圆,则A点在圆外,设MA交⊙O于C , 则∠MAN<∠MCN , 而∠MCN=∠MBN , 所以∠MAN<∠MBN.因此在B点射门为好.
【解析】考虑过M、N及A、B中任一点作圆,这里不妨过M、N、B作圆,则A点在圆外,设MA交⊙O于C , 则∠MAN<∠MCN , 而∠MCN=∠MBN , 所以∠MAN<∠MBN.因此在B点射门为好. .
.
在真正的足球比赛中情况比较复杂,这里仅用数学方法从两点的静止状态来考虑,如果两个点到球门的距离相差不大,要确定较好的射门位置,关键是看这两点各自对球门MN的张角大小,当张角较小时,则容易被对方守门员拦截.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
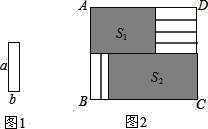
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙A,⊙B的半径分别为1cm,2cm,圆心距AB为5cm.如果⊙A由图示位置沿直线AB向右平移2cm,则此时该圆与⊙B的位置关系是( )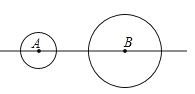
A.外离
B.相交
C.外切
D.内含
查看答案和解析>>
科目:初中数学 来源: 题型:
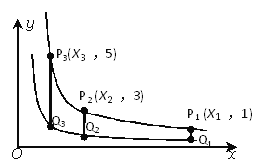
【题目】如图,函数y=![]() 和y=
和y=![]() 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
【答案】![]()
【解析】由题意得,P2012(x2012,4023),因为点P2012在y=![]() 的图象上,所以x2012=
的图象上,所以x2012=![]() ,把x2012=
,把x2012=![]() 代入 y=
代入 y=![]() 中得y2012=
中得y2012=![]() =
=![]() ,故答案为
,故答案为![]() .
.
【题型】填空题
【结束】
17
【题目】已知y是x的反比例函数,且当x=-4时,y=![]() ,
,
(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
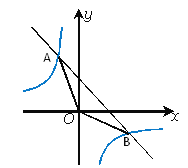
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
【答案】8![]()
【解析】整体分析:
联立方程y=![]() 和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=
和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=![]() ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.
解:把y=![]() 代入y= - x+4得,
代入y= - x+4得,
![]() = - x+4,
= - x+4,
解得x1=2+![]() ,x2=2-
,x2=2-![]() .
.
所以y1=2-![]() ,y2=2+
,y2=2+![]() .
.
则A(2-![]() ,2+
,2+![]() ),B(2+
),B(2+![]() ,2-
,2-![]() ),
),
所以△OAB的面积=![]() ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)==![]() ×4
×4![]() ×4
×4![]() =
=![]() .
.
【题型】解答题
【结束】
19
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.

(1)求m及k的值;
(2)不解关于x、y的方程组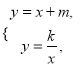 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-12所示,等腰三角形ABC的底边长为8 cm,腰长为5 cm,一动点P在底边上从点B向点C以0.25 cm/s的速度移动,请你探究:当点P运动几秒时,点P与顶点A的连线AP与腰垂直?

图17-Z-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
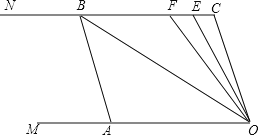
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
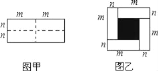
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;
方法二: .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com