
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
【答案】
(1)
证明:如图1中
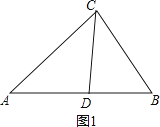
∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
∵CD平分∠ACB,
∴∠ACD=∠BCD= ![]() ∠ACB=40°,
∠ACB=40°,
∴∠ACD=∠A=40°,
∴△ACD为等腰三角形,
∵∠DCB=∠A=40°,∠CBD=∠ABC,
∴△BCD∽△BAC,
∴CD是△ABC的完美分割线.
(2)
解:①当AD=CD时,如图2
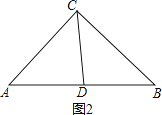 ,
,
∠ACD=∠A=45°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
②当AD=AC时,如图3中
 ,
,
∠ACD=∠ADC= ![]() =66°,
=66°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°.
③当AC=CD时,如图4中

∠ADC=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∵∠ADC>∠BCD,矛盾,舍弃.
∴∠ACB=96°或114°.
(3)
证明:由已知AC=AD=2,
∵△BCD∽△BAC,
∴ ![]() ,设BD=x,
,设BD=x,
∴( ![]() )2=x(x+2),
)2=x(x+2),
∵x>0,
∴x= ![]() ﹣1,
﹣1,
∵△BCD∽△BAC,
∴ ![]() =
= ![]() ,
,
∴CD= ![]() ×2=
×2= ![]() ﹣
﹣ ![]() .
.
【解析】(1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可.(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出∠ACB即可.(3)设BD=x,利用△BCD∽△BAC,得 ![]() ,列出方程即可解决问题.本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是理解题意,学会分类讨论思想,属于中考常考题型.
,列出方程即可解决问题.本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是理解题意,学会分类讨论思想,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C
B.点D或点E
C.线段DE(异于端点) 上一点
D.线段CD(异于端点) 上一点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点。
(1) 求证:四边形EFCD是菱形;(2)如果AB=10,求D、F两点间的距离。
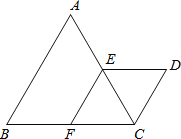
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.

(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为![]() 秒.
秒.
①若△NPH的面积为1,求![]() 的值;
的值;
②点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处由生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0,9,tan25°≈0.5, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com