练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了解七年级学生的身体素质情况，体育老师对该年级部分学生进行了一分钟跳绳次数的测试，并把测试成绩绘制成如图所示的频数表和频数直方图（每组含前一个边界值，不含后一个边界值）．

    （1）参加测试的学生有多少人？

    （2）求，的值，并把频数直方图补充完整．

    （3）若该年级共有名学生，估计该年级学生一分钟跳绳次数不少于次的人数．

    【答案】（1）40；（2）， ，图详见解析；（3）216

    【解析】

    （1）根据组别在100~120的频数和频率进行计算即可得到答案；

    （2）由（1）得到的总人数乘以a，b两项中的频率，即可得到答案；

    （3）320乘以不少于次的频率，即可得到答案.

    （1）（人）

    即参加测试的学生有人．

    （2）

    （3）

    即估计该年级学生一分钟跳绳次数在次（含次）以上的人数有人．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一个圆的半径为6cm,这个圆的内接正六边形的周长和面积各是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为2 cm，△PMN是一块直角三角板(∠N=30°)，PM＞2 cm，PM与BC均在直线l上，开始时M点与B点重合，将三角板向右平行移动，直至M点与C点重合为止.设BM=x cm，三角板与正方形重叠部分的面积为y cm2.

    下列结论：

    ①当0≤x≤时，y与x之间的函数关系式为y= x2；

    ②当时，y与x之间的函数关系式为y=2x-；

    ③当MN经过AB的中点时，y= (cm2)；

    ④存在x的值，使y= S正方形ABCD(S正方形ABCD表示正方形ABCD的面积).

    其中正确的是______(写出所有正确结论的序号).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，A（a，0），C（0，c）且满足：，长方形ABCO在坐标系中（如图1），点O为坐标系的原点．

    （1）求点B的坐标．

    （2）如图2，若点M从点A出发，以2个单位/秒的速度向右运动（不超过点O），点N从原点O出发，以1个单位/秒的速度向下运动（不超过点C），设M、N两点同时出发，在它们运动的过程中，四边形MBNO的面积是否发生变化？若不变，求其值；若变化，求变化的范围．

    （3）如图3，E为x轴负半轴上一点，且∠CBE＝∠CEB，F是x轴正半轴上一动点，∠ECF的平分线CD交BE的延长线于点D，在点F运动的过程中，请探究∠CFE与∠D的数量关系，并说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

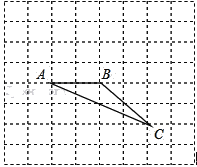
    【题目】如图在8×8的正方形网格中，△ABC 的顶点在边长为1的小正方形的顶点上．

    （1）填空：∠ABC=　 　，BC=　 　；

    （2）若点A在网格所在的坐标平面里的坐标为（1，﹣2），请你在图中找出一点D，并作出以A、B、C、D四个点为顶点的平行四边形，求出满足条件的D点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列资料，并解决问题.

    地球上的水包括大气水、地表水和地下水三大类，地表水可以分为海洋水和陆地水，陆地水又可分为冰川、河流、湖泊等。地球上的水总体积是14.2亿，其中，海洋水约占96.53%以上，淡水约占2.53%，而在淡水中，大部分在两极的冰川、冰盖和地下水的形式存在，其中冰川、冰盖占77.2%，地下水占22.4%，而人类可以利用的水还不到1%.

    我国是世界上严重缺水的国家之一，年水资源总量居世界第六位，人均占有水量仅为左右，只相当于世界人均的，居世界第110位，中国已被联合国列为13个贫水国之一.

    图1是我国2006年至2015年水资源总量变动趋势图，全国用水量由农业用水、工业用水、生活用水和生态补水四部分组成，表1是2015年我国四类用水量统计表.

    表1 2015年四类用水统计表

    用水类别

    用水量(亿立方米)

    所占百分比

    农业用水

    3903.9

    63.17%

    工业用水

    1380.6

    22.34%

    生活用水

    790.5

    12.79%

    生态补水

    105.0

    1.70%

    解决问题：

    (1)根据国外的经验，一个国家的用水量超过其水资源总量20%，就有可能发生“水危机”.依据这个标准，请你计算2015年我国是否属于可能发生“水危机”行列？

    (2)第四十七届联合国大会作出决议，确定每年3月22日为“世界水日”.我国水利部确定每年的3月22日至28日是“中国水周”.我国纪念“世界水日”和“中国水周”宣传活动的主题是“实施国家节水行动，建设节水型社会”.小亮作为学校的节水行动宣传志愿者，对他所在学校部分学生进行了“节水在行动”的随机调查，表2是问卷调查表，并将调查结果绘制成图2和图3所示的统计图(均不完整)，请根据统计图提供的信息，解答下列问题：

    ①参与本次调查的学生人数有________人(直接写出答案)；

    ②补全条形统计图；在扇形统计图中，观点的百分比是_______(直接写出答案)；

    表2：节水问卷调查表

    你好，请在表格中选择一项你对节水的认识，在其后面打“√”，非常感谢你的合作.

    代码

    观点

    A

    水费低，不需要节水

    B

    节水意识薄弱，认为水资源充足

    C

    缺乏社会责任意识，节水与我无关

    D

    知道节水的重要性，并有节水的好习惯

    ③若该学校共有800名学生，请估计其中“知道节水的重要性，并有节水的好习惯”的有多少人？

    ④谈一谈你对节约用水的看法.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    （1）；

    （2）；

    （3）；

    （4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰直角三角形ABC，AB=BC，直角顶点B在直线PQ上，且AD⊥PQ于D，CE⊥PQ于E．

    （1）△ADB与△BEC全等吗？为什么？

    （2）图1中，AD、DE、CE有怎样的等量关系？说明理由．

    （3）将直线PQ绕点B旋转到如图2所示的位置，其他条件不变，那么AD、DE、CE有怎样的等量关系？直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD的两个外角∠CBE，∠CDF的平分线交于点G，若∠A=52°，∠DGB=28°，则∠DCB的度数是（　　）

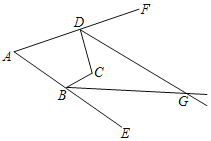
    A. 152°B. 128°C. 108°D. 80°

    查看答案和解析>>

    同步练习册答案