练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情


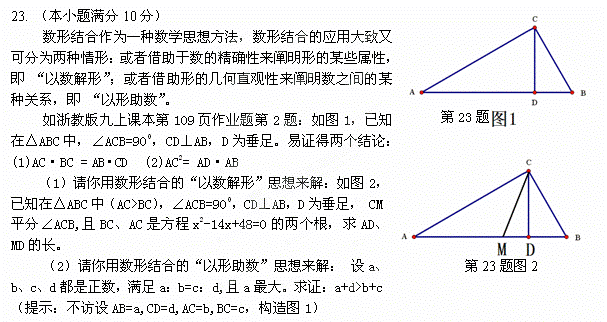
    解：（1）显然，方程x2-14x+48=0的两根为6和8，

    又AC>BC
    ∴AC=8，BC=6
    由勾股定理AB=10
    △ACD∽△ABC，得AC2= AD·AB
    ∴AD=6.4   
    ∵CM平分∠ACB
    ∴AM：MB=AC：CB
    解得，AM=-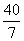
    ∴MD=AD-AM=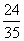

    （2）解：不访设AB=a,CD=d,AC=b,BC=c

    由三角形面积公式，得AB·CD=AC·BC
    2AB·CD=2AC·BC          

    又勾股定理，得AB2=AC2+BC2
    ∴AB2+2AB·CD =AC2+BC2+2AC·BC(等式性质)
    ∴AB2+2AB·CD =（AC+BC）2-

    ∴AB2+2AB·CD+CD2 >（AC+BC）2

    ∴(AB+CD) 2 >（AC+BC）2
    又AB、CD、AC、BC均大于零
    ∴AB+CD>AC+BC即a+d>b+c


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如上图2，AO＝8cm，PO＝4cm，∠POB＝60°，点P绕着点O以x度／秒的速度逆时针旋转一周停止，同时点Q沿直线BA自点B以ycm／秒的速度向点A运动，当点Q到达点A时，∠POQ恰好等于90°，则x：y＝　  ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


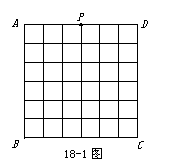
    如图18-1，正方形ABCD是一个6 × 6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图18-2的程序移动．

    （1）请在图18-1中画出光点P经过的路径；

    （2）求光点P经过的路径总长（结果保留π）．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    反比例函数图象上有三个点，，，其中，则，，的大小关系是               。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


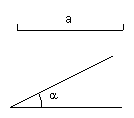
      （1）画图，已知线段a和锐角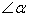，求作Rt△ABC，使它的一边为a，一锐角为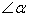（不写作法，要保留作图痕迹，作出其中一个满足条件的直角三角形即可）。

     （2）回答问题：

            满足上述条件的大小不同的共有          种。

            若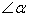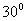＝，求最大的Rt△ABC的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在方格纸中有四个图形＜1＞、＜2＞、＜3＞、＜4＞，其中面积相等的图形是（　　）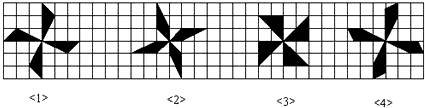

    　  A．＜2＞和＜3＞   B． ＜1＞和＜2＞      C． ＜2＞和＜4＞      D． ＜1＞和＜4＞

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的一元二次方程有解，求k的取值范围　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数据70、71、72、73、74的方差是（    ）

    A、     B、2     C、     D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从1，2，3，…9共9个数字中任取一个数字，取出数字为奇数的概率是　     　.

    查看答案和解析>>

    同步练习册答案