Question

下列各图中，E，F，G，H分别是AB，BC，CD，DA中点，
（1）如图1，求证：四边形EFGH是平行四边形
（2）如图2，当AC和BD满足条件________时，四边形EFGH是矩形（不必证明）如图3，当AC和BD满足条件________时，四边形EFGH是菱形（不必证明）
（3）如图4，当AC和BD满足条件________时，四边形EFGH是正方形，

Answer 1

（1）证明：连接BD、AC，两线交于O，
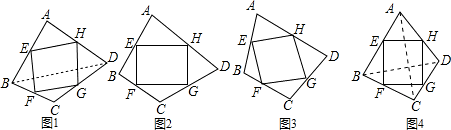
∵E，F，G，H分别是AB，BC，CD，DA中点，
∴EH∥BD，EH=BD，∥BD，FG=BD，
∴EH=FG，EH∥FG，
∴四边形EFGH是平行四边形．

（2）答案为：垂直，相等．

（3）答：垂直且相等，
证明：∵EH∥BD，AC⊥BD，
∴EH⊥AC，
∴∠EMC=90°，
∵E，F，G，H分别是AB，BC，CD，DA中点，
∴EF∥AC，EF=AC，
∴∠MEF=180°-90°=90°，
∵AC=BD，EH=BD，
∴EF=EH，
∵四边形EFGH是平行四边形，
∴平行四边形EFGH是正方形．
故答案为：垂直且相等．
分析：（1）根据三角形的中位线定理得出EH∥BD，EH=BD，∥BD，FG=BD，推出EH=FG，EH∥FG，即可得到平行四边形EFGH；
（2）根据平行线的性质得出∠EMO=∠AOB=∠HEF=90°，即可得出答案；根据EH=BD和EF=AC，即可得出答案；
（3）由平行四边形EFGH、∠EMO=∠AOB=∠HEF=90°和EH=EF即可得到正方形．
点评：本题主要考查对平行线的性质和判定，平行四边形的判定，菱形的判定，矩形的判定，正方形的判定，平行公理及推论，三角形的中位线等知识点的连接和掌握，综合运用这些性质进行证明是证此题的关键．题型较好，综合性强．