
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 (2013•邵阳)如图是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )
(2013•邵阳)如图是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )查看答案和解析>>
科目:初中数学 来源: 题型:
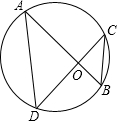 (2013•邵阳)如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是
(2013•邵阳)如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com