
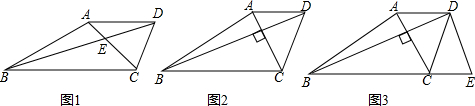
分析 (1)A同学:化成顶点式,即可得出答案;B同学:根据完全平方公式变形,再求出最值即可;
(2)过B、D、E三点作圆,作BF的垂直平分线交圆于点D1,即可得出答案;过B、D、F三点作圆,作BF的垂直平分线即可.
解答 解:(1)选择A同学:
S△DBE=$\frac{1}{2}$x$\sqrt{100-{x}^{2}}$=$\frac{1}{2}$$\sqrt{100{x}^{2}-{x}^{4}}$=$\frac{1}{2}$$\sqrt{-({x}^{2}-50)^{2}+2500}$,
当x2=50,即x=5$\sqrt{2}$,S△DBE取最大值25;
选择B同学.
方法一:S△DBE=$\frac{1}{2}$xy=$\frac{1}{4}$×2xy≤$\frac{1}{4}$(x2+y2)=25,
当x=y=5$\sqrt{2}$时,S△DBE取最大值25;
方法二:S△DBE=$\frac{1}{2}$xy=$\frac{1}{4}$[(x2+y2)-(x-y)2]=$\frac{1}{4}$[100-(x-y)2],
当(x-y)2=0,即x=y=5$\sqrt{2}$时,S△DBE取最大值25;
(2)如图: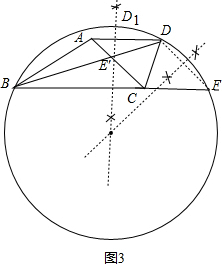
点D1即为所求的点;
如图:
如图2,
设BF的垂直平分线交⊙O于D1,M,交BF于N,连接BM、FM,FO,BO,
∵AC∥DF,
∴∠BDF=∠BEC=n°,
则∠BMF=180°-n°,
由圆周角定理得:∠BOF=2∠BMP=360°-2n°,
∵OB=OF,NM⊥BF,
∴BN=FN=$\frac{1}{2}$(a+b),∠BON=$\frac{1}{2}$∠BOF=180°-n°,
在Rt△BNO中,ON=$\frac{BN}{tan(180°-n°)}$=$\frac{\frac{1}{2}(a+b)}{tan(180°-n°)}$,
OD1=OB=$\frac{BN}{sin(180°-n°)}$=$\frac{\frac{1}{2}(a+b)}{sin(180°-n°)}$,
∴D1N=D1O-ON=$\frac{\frac{1}{2}(a+b)}{sin(180°-n°)}$-$\frac{\frac{1}{2}(a+b)}{tan(180°-n°)}$,
∴S梯形ABCD=$\frac{1}{2}$(AD1+BC)×D1N
=$\frac{1}{2}$(a+b)[$\frac{\frac{1}{2}(a+b)}{sin(180°-n°)}$-$\frac{\frac{1}{2}(a+b)}{tan(180°-n°)}$]
=$\frac{(a+b)^{2}}{4sinn°tann°}$
S梯形ABCD最大值为:$\frac{(a+b)^{2}}{4sinn°tann°}$.
点评 本题考查了三角形的外接圆,三角形的面积,完全平方公式,二次函数的最值,平行四边形的性质和判定,梯形的性质的应用,主要考查学生的动手操作能力和理解能力,难度偏大.此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com