
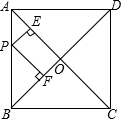
 如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于9cm.
如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于9cm. 分析 连结OP,如图,先根据正方形的性质得OA=OB=$\frac{1}{2}$BD=9cm,OA⊥OB,然后根据三角形面积公式得到$\frac{1}{2}$PE•OA+$\frac{1}{2}$PF•OB=$\frac{1}{2}$OA•OB=$\frac{1}{2}O{A}^{2}$,则变形后可得PE+PF=OA=9cm.
解答 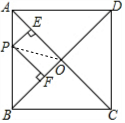 解:连接PO,
解:连接PO,
∵四边形ABCD为正方形,
∴AC⊥BD,∠BAC=45°,AO=OB=$\frac{1}{2}$BD=$\frac{1}{2}$×18=9,
∵PE⊥AO,PF⊥BO,
∴∠AOB=∠PEO=∠PFO=90°,△AEP是等腰直角三角形,
∴四边形PEOF是矩形,AE=PE,
∴PF=OE,
∴AO=AE+OE=PE+PF,
∴S△APO+S△OPB=S△ABO=$\frac{1}{2}$AO(PE+PF)=$\frac{1}{2}$×AO2,
则PE+PF=AO=9cm.
故答案为:9.
点评 本题考查了正方形的性质,利用面积法求线段的和,熟练掌握正方形的性质,确定其等量关系式是本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | (-3,0) | B. | (3,0) | C. | (a,0) | D. | (-b,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
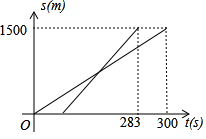 甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )
甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )| A. | 这是一次1500m的赛跑 | B. | 甲、乙两人中先到达终点的是乙 | ||
| C. | 甲、乙同时起跑 | D. | 甲在这次赛跑中的速度为5m/s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
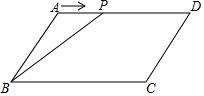 如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )
如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )| A. | y=-4x+2 | B. | y=-4x-2 | C. | y=2$\sqrt{3}$x | D. | y=$\sqrt{3}$x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com