
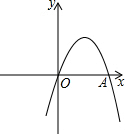
 如图,二次函数y=-x2+(1-2k)x+k+1图象与x轴相交于点O,A两点,
如图,二次函数y=-x2+(1-2k)x+k+1图象与x轴相交于点O,A两点,分析 (1)把(0,0)代入已知函数解析式即可求得k的值;
(2)利用面积法求得点B的纵坐标,然后由二次函数图象上点的坐标特征来求点B的横坐标即可.
解答 解:(1)如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于原点(0,0),
∴k+1=0,
解得,k=-1,
故该二次函数的解析式是:y=-x2+3x.
(2)∵△AOB是锐角三角形,
∴点B在第一象限.
设B(x,y)(x>0,y>0).
令-x2+3x=0,即(x-3)x=0,
解得x=3或x=0,
则点A(3,0),故OA=3.
∵锐角△AOB的面积等于3.
∴$\frac{1}{2}$OA•|y|=3,即$\frac{1}{2}$×3|y|=3,
解得,y=2.
又∵点B在二次函数图象上,
∴2=-x2+3x,
解得x=2或x=1(在对称轴的左侧,舍去).
故点B的坐标是(2,2).
点评 本题考查了二次函数的性质,解答(2)题时需要注意点B是位于这条抛物线的对称轴右边的图象上有一点.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
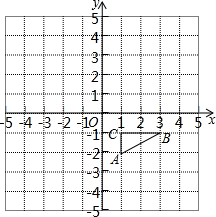 如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0)、C(3,0)、D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒$\frac{1}{2}$个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0)、C(3,0)、D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒$\frac{1}{2}$个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 关于直线对称的两个三角形一定全等 | |
| B. | 两个圆形纸片随意平放在水平桌面上构成轴对称图形 | |
| C. | 若两图形关于直线对称,则对称轴是对应点所连线的垂直平分线 | |
| D. | 等腰三角形一边上的高,中线及这边对角平分线重合 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
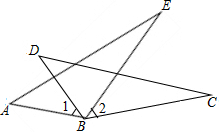 如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则可增加的条件是( )
如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则可增加的条件是( )| A. | ∠ABE=∠DBE | B. | ∠A=∠D | C. | ∠E=∠C | D. | ∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
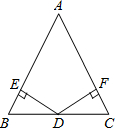 如图所示,在△ABC中,∠B=∠C,D为BC的中点,过点D分别向AB、AC作垂线段,则能够说明△BDE≌△CDF的理由是( )
如图所示,在△ABC中,∠B=∠C,D为BC的中点,过点D分别向AB、AC作垂线段,则能够说明△BDE≌△CDF的理由是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com