
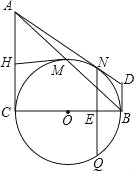
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
(1)求证:MH为⊙O的切线.
(2)若MH=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求⊙O的半径.
,求⊙O的半径.
(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.
【答案】(1)证明见解析;(2)2;(3)![]() .
.
【解析】
试题分析:(1)连接OH、OM,则OH为△ABC的中位线,进而可证明△COH≌△MOH,∴∠HCO=∠HMO=90°,从而可知MH是⊙O的切线;(2)由(1)可知MH=HC,H为AC中点,∠CMH=90°,可得AC=3,再利用三角函数可求得BC=4,故半径为2;(3)连接CN,AO,CN与AO相交于I,则AC=AN,又因为OC=ON,可知AO⊥CN, 利用面积可求得CI的长度,设CE为x,然后利用勾股定理可求得CE的长度,利用垂径定理即可求得NQ.
试题解析: (1)连接OH、OM,∵H是AC的中点,O是BC的中点,∴OH∥AB,∴∠COH=∠ABC,∠MOH=∠OMB,又∵OB=OM,∴∠OMB=∠MBO,∴∠COH=∠MOH,又∵OH=OH,∴△COH≌△MOH(SAS),∴∠HCO=∠HMO=90°,
∴MH是⊙O的切线;

(2)∵MH、AC是⊙O的切线,∴HC=MH=![]() ,∴AC=2HC=3,在Rt△ABC中,∠ACB=90°,∵
,∴AC=2HC=3,在Rt△ABC中,∠ACB=90°,∵![]() ,∴
,∴![]() ,∴BC=4,∴⊙O的半径为2;(3)连接OA、CN、ON,OA与CN相交于点I,∵AC与AN都是⊙O的切线,∴AC=AN,AO平分∠CAD,∴AO⊥CN,∵AC=3,OC=2,∴
,∴BC=4,∴⊙O的半径为2;(3)连接OA、CN、ON,OA与CN相交于点I,∵AC与AN都是⊙O的切线,∴AC=AN,AO平分∠CAD,∴AO⊥CN,∵AC=3,OC=2,∴![]() ,∵S△ACO=
,∵S△ACO=![]() AC·OC=
AC·OC=![]() AO·CI,∴CI=
AO·CI,∴CI=![]() ,∴CN=2CI=
,∴CN=2CI=![]() .设OE=x,由勾股定理可得:CN2﹣CE2=ON2﹣OE2,∴
.设OE=x,由勾股定理可得:CN2﹣CE2=ON2﹣OE2,∴ ![]() ,∴
,∴![]() ,∴
,∴![]() ,在Rt△CEN中,
,在Rt△CEN中,![]() ,∴NQ=2EN=
,∴NQ=2EN=![]() .
.



科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确命题的个数为( )个
①Rt△ABC中,已知两边长分别为3和4,则第三边为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
![]() ③三角形的三边分别为a,b,c若
③三角形的三边分别为a,b,c若![]() ,则∠C=90°
,则∠C=90°
④在△ABC中,∠A:∠B:∠C=1:5:6,则△ABC为直角三角形。
A、1 B、2 C、3 D、4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在网购越来越多地成为人们的一种消费方式,在2016年的“双11”网上促销活动中天猫和淘宝的支付交易额突破120000000000元,将数字120000000000用科学记数法表示为( )
A.1.2×1012
B.1.2×1011
C.0.12×1011
D.12×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com