
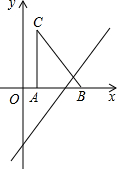 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).分析 (1)根据勾股定理得出AC,再写出点C坐标;
(2)根据题意,线段BC扫过的面积应为一平行四边形的面积,其高是AC的长,底是点C平移的路程.求当点C落在直线y=2x-6上时的横坐标即可.
解答  解:(1)∵点A、B的坐标分别为(1,0)、(4,0),
解:(1)∵点A、B的坐标分别为(1,0)、(4,0),
∴AB=3.
∵∠CAB=90°,BC=5,
∴AC=4.
∴点C的坐标是(1,4)
(2)如图所示,∵AC=4,
∴A′C′=4.
∵点C′在直线y=2x-6上,
∴2x-6=4,解得 x=5.
即OA′=5.
∴CC′=5-1=4.
∴S?BCC′B′=4×4=16 (面积单位).
即线段BC扫过的面积为16面积单位.
故答案为(1,4),16.
点评 本题考查了一次函数图象上点的坐标特征,平移的性质及一次函数的综合应用,解决本题的关键是明确线段BC扫过的面积应为一平行四边形的面积.


科目:初中数学 来源: 题型:解答题
 如图所示,一棵8米高的笔直的杉树在台风中被刮断,树顶C落在离树根B点4米处,科研人员要查看断痕A处的情况,在离树根B点1米的D处竖起一个梯子AD(点D、B、C在同一直线上),请问:这个梯子有多长?(结果请保留根号)
如图所示,一棵8米高的笔直的杉树在台风中被刮断,树顶C落在离树根B点4米处,科研人员要查看断痕A处的情况,在离树根B点1米的D处竖起一个梯子AD(点D、B、C在同一直线上),请问:这个梯子有多长?(结果请保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ab | B. | 3ab | C. | 3a2b2 | D. | 3a2b6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{24}÷\sqrt{3}=4$ | D. | $\sqrt{(-3)^{2}}=-3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com